
題目列表(包括答案和解析)
關于某設備的使用年限
x(年)和所支出的維修費用y(萬元)有如下統(tǒng)計資料:
若由資料知,
y對x呈線性相關關系,試求:(1)
回歸直線方程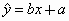 的回歸系數(shù)b與a;
的回歸系數(shù)b與a;
(2)
估計使用年限為10年時,維修費用約是多少?| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| |||||||
|
. |
| y |
. |
| x |
| 2 | 3 | 4 | 5 | 6 | |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 |
| b |
 |
| a |
| x(年) | 2 | 3 | 4 | 5 | 6 |
| y(萬元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| |||||||
|
 |
| a |
. |
| y |
. |
| x |
一、選擇題BBCAA BBAAD
11、-6 12、學.files/image205.gif) 13、4
13、4 學.files/image207.gif) 14、
14、學.files/image209.gif) 15、
15、學.files/image211.gif)
16.解:(1)在學.files/image136.gif) 中,由
中,由學.files/image142.gif) ,得
,得學.files/image215.gif) ……………………2分
……………………2分
又由正弦定理學.files/image217.gif) ………3分 得:
………3分 得:學.files/image219.gif) ………………4分
………………4分
(2)由余弦定理:學.files/image221.gif) 得:
得:學.files/image223.gif) ……6分
……6分
即學.files/image225.gif) ,解得
,解得學.files/image227.gif) 或
或學.files/image229.gif) (舍去),所以
(舍去),所以學.files/image231.gif) ………………8分
………………8分
所以,學.files/image146.gif)
學.files/image234.gif) ……………10分
……………10分
學.files/image236.gif) ,即
,即學.files/image238.gif) …………………… ……… ……12分
…………………… ……… ……12分
學.files/image240.gif)
學.files/image242.jpg)
18、(本小題滿分14分)
(1)連接BD,由已知有學.files/image244.gif)
得學.files/image246.gif) ………………………………(1分)
………………………………(1分)
又由ABCD是正方形,得:學.files/image248.gif) …(2分)
…(2分)
∵學.files/image250.gif) 與BD相交,∴
與BD相交,∴學.files/image251.gif) …………………………(3分)
…………………………(3分)
(2)延長DC至G,使CG=EB,,連結BG、D
學.files/image253.gif) ,∴四邊形EBGC是平行四邊形.
,∴四邊形EBGC是平行四邊形.
∴BG∥EC. ∴學.files/image255.gif) 就是異面直線BD1與CE所成角…………………………(5分)
就是異面直線BD1與CE所成角…………………………(5分)
在學.files/image257.gif) 中,
中,學.files/image259.gif)
學.files/image261.gif) …………………(6分)
…………………(6分)
學.files/image263.gif)
學.files/image265.gif)
學.files/image263.gif) 異面直線
異面直線 學.files/image267.gif) 與CE所成角的余弦值是
與CE所成角的余弦值是學.files/image269.gif) ……………………………(8分)
……………………………(8分)
(3)∵學.files/image271.gif) ∴
∴學.files/image273.gif)
又∵學.files/image275.gif) ∴ 點E到
∴ 點E到學.files/image277.gif) 的距離
的距離學.files/image279.gif) ……………(9分)
……………(9分)
有:學.files/image281.gif)
學.files/image283.gif) , ………………(11分)
, ………………(11分)
又由學.files/image285.gif) ,
設點B到平面
,
設點B到平面學.files/image172.gif) 的距離為
的距離為學.files/image287.gif) ,
,
則:學.files/image289.gif)
有:學.files/image291.gif) …………………………………(13分)
…………………………………(13分)
學.files/image293.gif) 所以:點B到平面
所以:點B到平面學.files/image172.gif) 的距離為
的距離為學.files/image295.gif) 。……………(14分)
。……………(14分)
19.解:(1)由題意可知當
學.files/image297.gif) ……3分
……3分
每件產(chǎn)品的銷售價格為學.files/image299.gif) ……………………………4分
……………………………4分
∴2009年的利潤 學.files/image301.gif)
學.files/image303.gif) ………………… 7分
………………… 7分
(2)學.files/image305.gif) ,……………………………11分
,……………………………11分
學.files/image307.gif) (萬元)13分
(萬元)13分
答:(略)…………………………………………………………………… 14分
20、解:(Ⅰ)圓學.files/image309.gif) , 半徑
, 半徑學.files/image311.gif)
學.files/image313.gif)
學.files/image315.gif) QM是P的中垂線,連結AQ,則|AQ|=|QP|
QM是P的中垂線,連結AQ,則|AQ|=|QP|
學.files/image317.gif) 又
又學.files/image319.gif) ,
,
根據(jù)橢圓的定義,點Q軌跡是以C(-學.files/image321.gif) ,0),A(
,0),A(學.files/image321.gif) ,0)為焦點,長軸長為2
,0)為焦點,長軸長為2學.files/image323.gif) 的
的
橢圓,………2分
由學.files/image325.gif) 因此點Q的軌跡方程為
因此點Q的軌跡方程為學.files/image327.gif) ………………4分
………………4分
(Ⅱ)(1)證明:當直線l垂直x軸時,由題意知:學.files/image329.gif)
不妨取學.files/image331.gif) 代入曲線E的方程得:
代入曲線E的方程得: 學.files/image333.gif)
即G(學.files/image335.gif) ,
,學.files/image335.gif) ),H(
),H(學.files/image335.gif) ,-
,-學.files/image335.gif) )有兩個不同的交點,………………5分
)有兩個不同的交點,………………5分
當直線l不垂直x軸時,設直線l的方程為:學.files/image337.gif)
由題意知:學.files/image339.gif)
由學.files/image341.gif)
學.files/image343.gif)
∴直線l與橢圓E交于兩點, 綜上,直線l必與橢圓E交于兩點…………8分
(2)由(1)知當直線l垂直x軸時,學.files/image345.gif)
學.files/image347.gif) ………………9分
………………9分
當直線l不垂直x軸時
設學.files/image349.gif) (1)知
(1)知 學.files/image351.gif)
學.files/image353.gif)
學.files/image355.gif)
學.files/image357.gif)
學.files/image359.gif) …………………………10分
…………………………10分
學.files/image361.gif)
當且僅當學.files/image363.gif) ,則取得“=”
,則取得“=”
學.files/image365.gif) ……………………12分
……………………12分
當k=0時,學.files/image367.gif) 綜上,△OGH的面積的最小值為
綜上,△OGH的面積的最小值為學.files/image369.gif) …14分
…14分
21.解:(1)在已知式中,當學.files/image371.gif) 時,
時,學.files/image373.gif)
∵學.files/image375.gif) ∴
∴學.files/image377.gif) …………2分
…………2分
當學.files/image379.gif) 時,
時,學.files/image193.gif) ①
① 學.files/image382.gif) ②
②
①-②得,學.files/image384.gif)
∵學.files/image386.gif) ∴
∴學.files/image388.gif) =
=學.files/image390.gif) ③
③
∵學.files/image377.gif) 適合上式…………4分 當
適合上式…………4分 當學.files/image379.gif) 時,
時, 學.files/image392.gif) ④
④
③-④得: 學.files/image394.gif)
∵學.files/image396.gif) ∴
∴學.files/image398.gif) ∴數(shù)列
∴數(shù)列學.files/image189.gif) 是等差數(shù)列,首項為1,公差為1,可得
是等差數(shù)列,首項為1,公差為1,可得學.files/image401.gif)
(2)假設存在整數(shù)學.files/image201.gif) ,使得對任意
,使得對任意 學.files/image191.gif) ,都有
,都有學.files/image203.gif) .
.
∵學.files/image401.gif) ∴
∴學.files/image404.gif)
∴學.files/image406.gif)
學.files/image408.gif)
∴學.files/image410.gif) ⑤……………………………………………8分
⑤……………………………………………8分
當學.files/image412.gif) (
(學.files/image414.gif) )時,⑤式即為
)時,⑤式即為學.files/image416.gif) ⑥
⑥
依題意,⑥式對學.files/image414.gif) 都成立,∴λ<1……………………………………10分
都成立,∴λ<1……………………………………10分
當學.files/image418.gif) (
(學.files/image414.gif) )時,⑤式即為
)時,⑤式即為學.files/image420.gif) ⑦
⑦
依題意,⑦式對學.files/image414.gif) 都成立, ∴
都成立, ∴學.files/image422.gif) ……………12分
……………12分
∴學.files/image424.gif) ∴存在整數(shù)
∴存在整數(shù)學.files/image426.gif) ,使得對任意
,使得對任意學.files/image191.gif) ,都有
,都有學.files/image203.gif) …14分
…14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com