
題目列表(包括答案和解析)
(本題滿分10分)
已知四棱錐 的底面為直角梯形,
的底面為直角梯形, //
//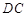 ,
, ,
,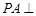 底面
底面 ,且
,且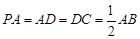 .
.
(Ⅰ)證明: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值的大小.
的余弦值的大小.

(本題滿分10分)
已知四棱錐 的底面為直角梯形,
的底面為直角梯形,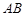 //
//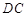 ,
,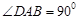 ,
,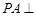 底面
底面 ,且
,且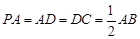 .
.
(Ⅰ)證明: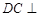 平面
平面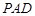 ;
;
(Ⅱ)求二面角 的余弦值的大小.
的余弦值的大小.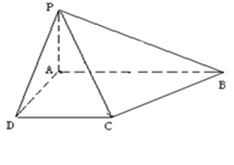
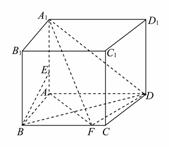
(本小題滿分14分)已知在直四棱柱ABCDA1B1C1D1中,底面ABCD為直角梯形,且滿足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8,E,F(xiàn)分別是線段A1A,BC上的點.
(1) 若A1E=5,BF=10,求證:BE∥平面A1FD.
(2) 若BD⊥A1F,求三棱錐A1AB1F的體積.
(本小題滿分14分)已知在直四棱柱ABCDA1B1C1D1中,底面ABCD為直角梯形,且滿足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8,E,F分別是線段A1A,BC上的點.
(1) 若A1E=5,BF=10,求證:BE∥平面A1FD.
(2) 若BD⊥A1F,求三棱錐A1AB1F的體積.
第Ⅰ卷
一、填空題:
1. {1,2,3}; 2.充分非必要;3.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image216.gif) ; 4.
; 4.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image218.gif) ; 5. 8; 6. (歷史) 5049; (物理)
; 5. 8; 6. (歷史) 5049; (物理) 2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image220.gif) ; 7. 1; 8.
; 7. 1; 8.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image222.gif)
9.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image224.gif) ;10.
;10.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image226.gif) ; 11.
; 11.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image228.gif) ; 12.
; 12.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image230.gif) ;13.
;13.2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image232.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image234.gif) ;14. 4.
;14. 4.
二、解答題:
15. 解:(1)因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image119.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image236.gif) …………(3分)
…………(3分)
得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image238.gif) (用輔助角得到
(用輔助角得到2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image240.gif) 同樣給分) ………(5分)
同樣給分) ………(5分)
又2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image117.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image121.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image242.gif) ……………………………………(7分)
……………………………………(7分)
(2)因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image244.gif) ………………………(9分)
………………………(9分)
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image246.gif) …………………………………………(11分)
…………………………………………(11分)
所以當(dāng)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image121.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image248.gif) 時,
時, 2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image250.gif) 的最大值為5+4=9 …………………(13分)
的最大值為5+4=9 …………………(13分)
故2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image123.gif) 的最大值為3 ………………………………………(14分)
的最大值為3 ………………………………………(14分)
16. (選歷史方向) 解: (1)表格為:
高 個
非高個
合 計
大 腳
5
2
7
非大腳
1
13
合 計
6
14
…… (3分)
(說明:黑框內(nèi)的三個數(shù)據(jù)每個1分,黑框外合計數(shù)據(jù)有錯誤的暫不扣分)
(2)提出假設(shè)H0: 人的腳的大小與身高之間沒有關(guān)系. …………………………… (4分)
根據(jù)上述列聯(lián)表可以求得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image253.gif) .…………………… (7分)
.…………………… (7分)
當(dāng)H0成立時,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image255.gif) 的概率約為0.005,而這里8.802>7.879,
的概率約為0.005,而這里8.802>7.879,
所以我們有99.5%的把握認(rèn)為: 人的腳的大小與身高之間有關(guān)系. ……………… (8分)
(3)
①抽到12號的概率為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image257.gif) ………………………………… (11分)
………………………………… (11分)
②抽到“無效序號(超過20號)”的概率為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image259.gif) …………………… (14分)
…………………… (14分)
(選物理方向) 解:(Ⅰ)在給定的直角坐標(biāo)系下,設(shè)最高點為A,入水點為B,
拋物線的解析式為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image261.gif) . …………………………… 2′
. …………………………… 2′
由題意,知O(0,0),B(2,-10),且頂點A的縱坐標(biāo)為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image263.gif) .…………… 4′
.…………… 4′
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image265.gif) 或
或2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image267.gif) ……………………………
8′
……………………………
8′
∵拋物線對稱軸在y軸右側(cè),∴2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image269.gif) ,又∵拋物線開口向下,∴a<0,
,又∵拋物線開口向下,∴a<0,
從而b>0,故有2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image271.gif) ……………………………9′
……………………………9′
∴拋物線的解析式為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image273.gif) . ……………………………10′
. ……………………………10′
(Ⅱ)當(dāng)運動員在空中距池邊的水平距離為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image127.gif) 米時,
米時,
即2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image275.gif) 時,
時,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image277.gif) , ……………………………12′
, ……………………………12′
∴此時運動員距水面的高為10-2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image279.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image281.gif) <5,因此,此次跳水會失誤.………………14′
<5,因此,此次跳水會失誤.………………14′
17. (1)證明:由直四棱柱,得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image283.gif) ,
,
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image285.gif) 是平行四邊形,所以
是平行四邊形,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image287.gif) …………………(3分)
…………………(3分)
而2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image289.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image291.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image139.gif) 面
面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image141.gif) ………(4分)
………(4分)
(2)證明:因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image293.gif) , 所以
, 所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image295.gif) ……(6分)
……(6分)
又因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image297.gif) ,且
,且2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image299.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image301.gif) ………
……(8分)
………
……(8分)
而2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image303.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image143.gif) …………………………(9分)
…………………………(9分)
(3)當(dāng)點2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image135.gif) 為棱
為棱2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image137.gif) 的中點時,平面
的中點時,平面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image145.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image037.gif) 平面
平面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image148.gif) …………………(10分)
…………………(10分)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image305.gif) 取DC的中點N,
取DC的中點N,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image307.gif) ,連結(jié)
,連結(jié)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image309.gif) 交
交2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image311.gif) 于
于2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) ,連結(jié)
,連結(jié)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image177.gif) .
.
因為N是DC中點,BD=BC,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image315.gif) ;又因為DC是面ABCD與面
;又因為DC是面ABCD與面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image317.gif) 的交線,而面ABCD⊥面
的交線,而面ABCD⊥面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image317.gif) ,
,
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image319.gif) ……………(12分)
……………(12分)
又可證得,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) 是
是2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image309.gif) 的中點,所以BM∥ON且BM=ON,即BMON是平行四邊形,所以BN∥OM,所以O(shè)M
的中點,所以BM∥ON且BM=ON,即BMON是平行四邊形,所以BN∥OM,所以O(shè)M2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image037.gif) 平面
平面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image323.gif) ,
,
因為OM?面DMC1,所以平面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image145.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image037.gif) 平面
平面2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image323.gif) ………………………(14分)
………………………(14分)
18. 解:(1)因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image326.gif) ,所以c=1……………………(2分)
,所以c=1……………………(2分)
則b=1,即橢圓2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image328.gif) 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image330.gif) …………………………(4分)
…………………………(4分)
(2)因為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image179.gif) (1,1),所以
(1,1),所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image333.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image335.gif) ,所以直線OQ的方程為y=-2x(6分)
,所以直線OQ的方程為y=-2x(6分)
又橢圓的左準(zhǔn)線方程為x=-2,所以點Q(-2,4) …………………………(7分)
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image337.gif) ,又
,又2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image339.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image341.gif) ,即
,即2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image343.gif) ,
,
故直線2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image345.gif) 與圓
與圓2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) 相切……………………………………………………(9分)
相切……………………………………………………(9分)
(3)當(dāng)點2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image179.gif) 在圓
在圓2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) 上運動時,直線
上運動時,直線2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image345.gif) 與圓
與圓2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) 保持相切 ………(10分)
保持相切 ………(10分)
證明:設(shè)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image350.gif) (
(2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image352.gif) ),則
),則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image354.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image356.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image358.gif) ,
,
所以直線OQ的方程為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image360.gif) ……………(12分)
……………(12分)
所以點Q(-2,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image362.gif) ) ………………
(13分)
) ………………
(13分)
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image364.gif) ,
,
又2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image366.gif) ,所以
,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image341.gif) ,即
,即2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image343.gif) ,故直線
,故直線2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image345.gif) 始終與圓
始終與圓2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image153.gif) 相切……(15分)
相切……(15分)
19.⑴解:函數(shù)的定義域為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image369.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image371.gif) (
(2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image373.gif) )…… (2分)
)…… (2分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image375.gif) ,則
,則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image377.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image379.gif) 有單調(diào)遞增區(qū)間
有單調(diào)遞增區(qū)間2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image369.gif) . ……………… (3分)
. ……………… (3分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image382.gif) ,令
,令2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image384.gif) ,得
,得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image386.gif) ,
,
當(dāng)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image388.gif) 時,
時,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image390.gif) ,
,
當(dāng)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image392.gif) 時,
時,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image377.gif) . ……………… (5分)
. ……………… (5分)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image379.gif) 有單調(diào)遞減區(qū)間
有單調(diào)遞減區(qū)間2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image396.gif) ,單調(diào)遞增區(qū)間
,單調(diào)遞增區(qū)間2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image398.gif) . ……………… (6分)
. ……………… (6分)
⑵解:(i)若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image375.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image379.gif) 在
在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image402.gif) 上單調(diào)遞增,所以
上單調(diào)遞增,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image404.gif) . ……… (7分)
. ……… (7分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image406.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image379.gif) 在
在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image396.gif) 上單調(diào)遞減,在
上單調(diào)遞減,在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image408.gif) 上單調(diào)遞增,
上單調(diào)遞增,
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image410.gif) . ………………
(9分)
. ………………
(9分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image412.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image379.gif) 在
在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image402.gif) 上單調(diào)遞減,所以
上單調(diào)遞減,所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image416.gif) .………… (10分)
.………… (10分)
綜上所述,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image418.gif) ……………… (12分)
……………… (12分)
(ii)令2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image420.gif) .若
.若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image375.gif) ,無解. ………………
(13分)
,無解. ………………
(13分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image406.gif) ,解得
,解得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image424.gif) . ……………… (14分)
. ……………… (14分)
若2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image412.gif) ,解得
,解得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image427.gif) . ………………
(15分)
. ………………
(15分)
故2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image008.gif) 的取值范圍為
的取值范圍為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image430.gif) . ……………… (16分)
. ……………… (16分)
20. (1)數(shù)表中第2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image432.gif) 行的數(shù)依次所組成數(shù)列的通項為
行的數(shù)依次所組成數(shù)列的通項為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image434.gif) ,則由題意可得
,則由題意可得
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image436.gif) … (2分)
… (2分)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image438.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image440.gif) (其中
(其中2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image442.gif) 為第
為第2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image444.gif) 行數(shù)所組成的數(shù)列的公差)
(4分)
行數(shù)所組成的數(shù)列的公差)
(4分)
(2)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image446.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image448.gif) 第一行的數(shù)依次成等差數(shù)列,由(1)知,第2行的數(shù)也依次成等差數(shù)列,依次類推,可知數(shù)表中任一行的數(shù)(不少于3個)都依次成等差數(shù)列. ……………… (5分)
第一行的數(shù)依次成等差數(shù)列,由(1)知,第2行的數(shù)也依次成等差數(shù)列,依次類推,可知數(shù)表中任一行的數(shù)(不少于3個)都依次成等差數(shù)列. ……………… (5分)
設(shè)第2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image444.gif) 行的數(shù)公差為
行的數(shù)公差為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image451.gif) ,則
,則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image453.gif) ,則
,則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image455.gif) …………… (6分)
…………… (6分)
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image457.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image459.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image461.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image463.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image465.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image467.gif) (10 分)
(10 分)
(3)由2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image469.gif) ,可得
,可得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image471.gif)
所以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image473.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image475.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image477.gif) ……………… (11分)
……………… (11分)
令2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image479.gif) ,則
,則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image481.gif) ,所以
,所以 2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image483.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image485.gif) ………… (13分)
………… (13分)
要使得2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image487.gif) ,即
,即2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image489.gif) ,只要
,只要2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image491.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image493.gif) ,
,
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image495.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image497.gif) ,所以只要
,所以只要2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image499.gif) ,
,
即只要2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image501.gif) ,所以可以令
,所以可以令2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image503.gif)
則當(dāng)2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image505.gif) 時,都有
時,都有2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image487.gif) .
.
所以適合題設(shè)的一個函數(shù)為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image508.gif) (16分)
(16分)
第Ⅱ卷(附加題 共40分)
1. (1)設(shè)動點P的坐標(biāo)為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image510.gif) ,M的坐標(biāo)為
,M的坐標(biāo)為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image512.gif) ,
,
則2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image514.gif) 即為所求的軌跡方程. …………(6分)
即為所求的軌跡方程. …………(6分)
(2)由(1)知P的軌跡是以(2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image516.gif) )為圓心,半徑為
)為圓心,半徑為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image518.gif) 的圓,易得RP的最小值為1
的圓,易得RP的最小值為1
.……(10分)
2. 2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image520.gif) ,|x-a|<l,
,|x-a|<l,
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image522.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image524.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image526.gif) ,
…………………………………………………5分
,
…………………………………………………5分
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image528.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image530.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image532.gif) ………………………10分
………………………10分
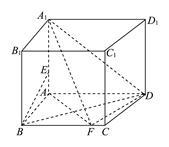
3. 證明:以2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image534.gif) 為坐標(biāo)原點
為坐標(biāo)原點2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image536.gif) 長為單位長度,如圖建立空間直角坐標(biāo)系,則各點坐標(biāo)為
長為單位長度,如圖建立空間直角坐標(biāo)系,則各點坐標(biāo)為
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image538.gif) .
.
(1)解:因2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image540.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image542.gif)
所以,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image057.gif) 與
與2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image206.gif) 所成的角余弦值為
所成的角余弦值為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image544.gif) …………………………………5分
…………………………………5分
(2)解:在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image546.gif) 上取一點
上取一點2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image548.gif) ,則存在
,則存在2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image550.gif) 使
使2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image552.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image554.gif)
要使2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image556.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image558.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image560.gif) 為
為
所求二面角2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image210.gif) 的平面角.
的平面角.
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image562.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image564.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image566.gif) …………………………………10分
…………………………………10分
另解:可以計算兩個平面的法向量分別為:平面AMC的法向量2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image568.gif) ,平面BMC的法向量為
,平面BMC的法向量為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image570.gif) ,
,2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image572.gif) =
=2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image574.gif) , 所求二面角
, 所求二面角2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image210.gif) 的余弦值為-
的余弦值為-2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image574.gif) .
.
4. (1)記事件A為“任取兩張卡片,將卡片上的函數(shù)相加得到的函數(shù)是奇函數(shù)”,由題意知2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image577.gif) ………………………………4分
………………………………4分
(2)ξ可取1,2,3,4.
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image579.gif) ,
,
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image581.gif) ;………………8分
;………………8分
故ξ的分布列為
ξ
1
2
3
4
P
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image583.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image585.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image587.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image589.gif)
2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image591.gif)
答:ξ的數(shù)學(xué)期望為2008~2009學(xué)年度第二學(xué)期周周練高三數(shù)學(xué)試題.files/image593.gif) ………………………………10分
………………………………10分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com