欧美日韩在线免费观看视频,欧美激情一级欧美精品,亚洲色图13p

2．已知函數(shù)f(x)是定義在閉區(qū)間[-a.a](a > 0)上的奇函數(shù)..則F(x)最大值與最小值之和為 A．1 B．2 C．3 D．0 的樣本.那么高三年級(jí)應(yīng)抽人數(shù)為 A．16 B．40 C．20 D．25 【查看更多】

題目列表(包括答案和解析)

已知函數(shù)f(x)的定義域D，且f(x)同時(shí)滿(mǎn)足以下條件：

①f(x)在D上單調(diào)遞增或單調(diào)遞減；

②存在區(qū)間[a，b]D(其中a＜b，使得f(x)在區(qū)間[a，b]的值域是[a，b]，那么我們把函數(shù)f(x)(x∈D)叫做閉函數(shù)．

(1)求閉函數(shù)y＝－x³符合條件②的區(qū)間[a，b]；

(2)判斷函數(shù)y＝2x－lgx是不是閉函數(shù)，若是，請(qǐng)說(shuō)明理由，并找出區(qū)間[a，b]；若不是，請(qǐng)說(shuō)明理由；

(3)若y＝k＋是閉函數(shù)，求實(shí)數(shù)k的取值范圍．

查看答案和解析>>

已知f(x)是定義在集合M上的函數(shù)．若區(qū)間D⊆M，且對(duì)任意x₀∈D，均有f(x₀)∈D，則稱(chēng)函數(shù)f(x)在區(qū)間D上封閉．
(1)判斷f(x)＝x－1在區(qū)間[－2,1]上是否封閉，并說(shuō)明理由；
(2)若函數(shù)g(x)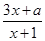＝在區(qū)間[3,10]上封閉，求實(shí)數(shù)a的取值范圍；
(3)若函數(shù)h(x)＝x³－3x在區(qū)間[a，b](a，b∈Z，且a≠b)上封閉，求a，b的值．

查看答案和解析>>

在區(qū)間[3,10]上封閉，求實(shí)數(shù)a的取值范圍；
(3)若函數(shù)h(x)＝x³－3x在區(qū)間[a，b](a，b∈Z，且a≠b)上封閉，求a，b的值．

查看答案和解析>>

已知函數(shù)f(x)的定義域?yàn)镈，且f(x)同時(shí)滿(mǎn)足以下條件：

①f(x)在D上單調(diào)遞增或單調(diào)遞減；

②存在區(qū)間[a，b]D，使得f(x)在[a，b]上的值域是[a，b]，那么我們把函數(shù)f(x)(x∈D)叫做閉函數(shù)．

(1)求閉函數(shù)y＝－x³符合條件2的區(qū)間[a，b]．

(2)判斷函數(shù)y＝2x－lgx是不是閉函數(shù)？若是，請(qǐng)說(shuō)明理由，并找出區(qū)間[a，b]；若不是，請(qǐng)說(shuō)明理由．

(3)若y＝k＋是閉函數(shù)，求實(shí)數(shù)k的取值范圍．

查看答案和解析>>

已知y＝f(x)(x∈D，D為此函數(shù)的定義域)同時(shí)滿(mǎn)足下列兩個(gè)條件：①函數(shù)f(x)在D內(nèi)單調(diào)遞增或單調(diào)遞減；②如果存在區(qū)間，使函數(shù)f(x)在區(qū)間[a，b]上的值域?yàn)閇a，b]，那么稱(chēng)y＝f(x)，x∈D為閉函數(shù)；

(1)判斷函數(shù)是否為閉函數(shù)？并說(shuō)明理由；

(2)求證：函數(shù)y＝－x³()為閉函數(shù)；

(3)若是閉函數(shù)，求實(shí)數(shù)k的取值范圍．

查看答案和解析>>

1.A 2.B 3.C 4.C 5.A 6.C 7.D 8.D 9.A 10.C

11.80 12.30 13.c 14. 15. .

三、解答題

16．解：（1）(ka+b)²=3(a－kb)² k²++2ka?b=3(1+k²－2ka?b)

∴a?b= 當(dāng)k=1時(shí)取等號(hào). （6分）

（2）a?b=

∴時(shí)，a?b=取最大值1. （12分）

17．解：（1）由已知有x_n₊₁－1=2(x_n－1)

∴{x_n－1}是以1為首項(xiàng)以2為公比的等比數(shù)列，又x₁=2.

∴x_n－1=2ⁿ^－1 ∴x_n=1+2ⁿ^－1(n∈N*) （6分）

（2）由

又當(dāng)n∈N*時(shí)，x_n≥2故點(diǎn)（x_n，y_n）在射線(xiàn)x+y=3（x_n≥2）上。（12分）

18．解：（1）記乙勝為事件A，則P（A）=


（2）解法一：由題意：(x，y)=（1，4）或（1，3）或（1，2）或（1，1）或（2，3）或（2，2）或（2，1）或（3，2）或（3，1）或（4，1）。故當(dāng)x=1，y=4時(shí)，x+2y取最大值9，即x=1， y=4時(shí)乙獲勝的概率最大為.（12分）解法二：令t=x+2y，，（x,y）取值如圖所示，由線(xiàn)性規(guī)劃知識(shí)知x=1,y=4時(shí)，t最大，故x=1，y=4，乙獲勝的概率最大為. （12分） 19．解（1）設(shè)正三棱柱―的側(cè)棱長(zhǎng)為．取中點(diǎn)，連．是正三角形，．又底面側(cè)面，且交線(xiàn)為．側(cè)面．……3分連，則直線(xiàn)與側(cè)面所成的角為．在中，，解得．此正三棱柱的側(cè)棱長(zhǎng)為． ……5分（2）過(guò)作于，連，側(cè)面．為二面角的平面角．…7分在中，，又，．又在中，．故二面角的大小為． ……9分（3）解法1：由（2）可知，平面,平面平面，且交線(xiàn)為，過(guò)作于，則平面．……11分在中，．為中點(diǎn)，點(diǎn)到平面的距離為． ………… 13 20．解： 21．解：（1） ∴，故橢圓Q_n的焦距2c_n≥1. （4分）（2）（i）設(shè)P_n(x_n，y_n)，則同步練習(xí)冊(cè)答案全品作業(yè)本答案同步測(cè)控優(yōu)化設(shè)計(jì)答案長(zhǎng)江作業(yè)本同步練習(xí)冊(cè)答案同步導(dǎo)學(xué)案課時(shí)練答案仁愛(ài)英語(yǔ)同步練習(xí)冊(cè)答案一課一練創(chuàng)新練習(xí)答案時(shí)代新課程答案新編基礎(chǔ)訓(xùn)練答案能力培養(yǎng)與測(cè)試答案更多練習(xí)冊(cè)答案國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) \| 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) \| 電信詐騙舉報(bào)專(zhuān)區(qū) \| 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) \| 涉企侵權(quán)舉報(bào)專(zhuān)區(qū) 違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com 版權(quán)聲明：本站所有文章，圖片來(lái)源于網(wǎng)絡(luò)，著作權(quán)及版權(quán)歸原作者所有，轉(zhuǎn)載無(wú)意侵犯版權(quán)，如有侵權(quán)，請(qǐng)作者速來(lái)函告知，我們將盡快處理，聯(lián)系qq：3310059649。 ICP備案序號(hào): 滬ICP備07509807號(hào)-10 鄂公網(wǎng)安備42018502000812號(hào) 感谢您访问我们的网站，您可能还对以下资源感兴趣：亚洲高清精品视频国产精品美女久久久久人\| 国产精品亚洲综合\| 超碰97在线播放\| 日韩欧美一区二区在线观看\| 国产情侣第一页\| 日韩精品一区二区三区色欲av\| 999久久久精品视频\| 亚洲AV无码国产成人久久\| www.99re7\| 一级黄色片在线\| 在线观看免费视频一区二区三区\| 成人在线视频亚洲\| 伊人久久大香伊蕉在人线观看热v\| 中国av一区\| 一二三区精品\| 99久久国产综合精品女不卡\| 一个色综合av\| 日韩三级.com\| 欧美极度另类性三渗透\| 99久久精品免费看国产四区 \| 一区二区三区韩国免费中文网站\| 午夜精品免费\| 国产不卡在线视频\| 成人免费公开视频\| 日本高清一区二区视频\| 夜夜春很很躁夜夜躁\| 亚洲天堂视频在线播放\| 亚州av电影免费在线观看\| 成人女同在线观看\| 精品欧美午夜寂寞影院\| 亚洲深夜影院\| 久久免费看少妇高潮\| 91国产免费观看\| 色综合影院在线\| 91久久精品日日躁夜夜躁国产\| 伊人久久99\| 杨幂一区二区国产精品\| 国产精品99re\| 亚洲成人天堂\| 欧美日韩国产网站\| 97色伦图片97综合影院\| 成人午夜在线视频\| 日韩欧美视频一区二区三区\| 中文字幕国产亚洲2019\| 99久久99久久\| 日韩中文字幕免费在线\| 国产中文av在线\| 成人福利小视频\| 交100部在线观看\| 青青草原综合久久大伊人精品\| 激情五月播播久久久精品\| 午夜欧美视频在线观看\| 在线看日韩欧美\| 成人蜜桃视频\| 亚洲天堂av线\| 日本中文字幕免费\| 久草在现在线\| 久久亚洲高清\| 麻豆成人av\| 国产精品igao网网址不卡\| 日韩欧美一区二区一幕\| 男同在线观看\| 国产96在线亚洲\| 视频一区二区国产\| 亚洲成年人影院\| xxxx性欧美\| 精品日产一区2区三区黄免费\| 999精品视频在线\| 天堂网一区二区三区\| 成人高清免费观看mv\| 亚洲国产精品免费视频\| 奇米影视在线99精品\| 亚洲大片在线观看\| 欧美大胆a视频\| 亚洲一卡二卡三卡四卡无卡网站在线看\| 99精品视频免费版的特色功能\| 一级久久久久久\| 国产鲁鲁视频在线观看特色\| 欧洲杯半决赛直播\| 久久综合九色综合久久久精品综合\| 日韩欧美高清一区\| 亚洲va欧美va国产综合剧情\| www.亚洲高清\| 亚洲图片小说视频\| 男男gaygays亚洲\| 欧美成人嫩草网站\| 亚洲欧美日韩精品久久久久\| 久久精品国产成人\| 一区二区三区视频\| 林心如三级全黄裸体\| 亚洲欧洲成人\| 日韩美脚连裤袜丝袜在线\| caoporn国产精品\| 亚洲国产97在线精品一区\| 国产99在线播放\| 久久久久久婷婷\| 性感美女视频一二三\| 国产精品调教视频\| 26uuu欧美\| 在线不卡国产精品\| 中文字幕在线亚洲三区\| 欧美激情一区二区视频\| 二区三区在线观看\| 中文亚洲免费\| 欧美性受xxxx黑人xyx\| 国产日产欧美精品\| 肉丝美足丝袜一区二区三区四\| 精品国产无码AV\| 日韩中文字幕无砖\| 久久久综合精品\| 日韩中文字在线\| 日韩精品在线中文字幕\| 97久久久久久久\| av鲁丝一区鲁丝二区鲁丝三区\| 日韩中文不卡\| 日本乱子伦xxxx\| √新版天堂资源在线资源\| 91成人精品\| 精品国产91乱高清在线观看\| 国产精品美女免费看\| 国产黄色一区二区三区\| 在线香蕉视频\| 色婷婷色综合\| 精品国产精品三级精品av网址\| 国产精品黄页免费高清在线观看\| 日韩av福利在线观看\| 在线看的你懂得\| 99久久99久久精品国产片果冰\| 无吗不卡中文字幕\| 成人黄色午夜影院\| 亚洲av综合一区二区\| 日本在线观看视频\| 老司机精品视频网站\| 欧美va日韩va\| 免费观看中文字幕\| 久久久久久无码午夜精品直播\| 欧美大陆国产\| 久久久久久久久岛国免费\| 欧美激情一区二区三区成人 \| 57pao成人永久免费视频\| 国产无色aaa\| 亚洲尤物在线视频\| 亚洲大胆视频\| 欧美zozo另类异族\| 男女激烈动态图\| 888奇米影视\| 亚洲小说图片\| 欧美天天综合色影久久精品\| 韩国成人一区\| 九九热国产视频\| 国产精品高清一区二区\| 国产精品久久久久久久久搜平片\| 日韩av日韩在线观看\| 好吊一区二区三区视频\| 亚洲www色\| 高清在线成人网\| 欧美日韩国产成人在线观看\| 97中文字幕在线观看\| 日本视频不卡\| 国产毛片精品国产一区二区三区\| 久久精品福利视频\| 1314成人网\| av网站免费在线观看\| 国产一区二三区好的\| 久久人人爽人人爽人人片亚洲\| 久久久久久蜜桃一区二区\| 伦理片一区二区三区\| 视频在线观看91\| 尤物九九久久国产精品的特点 \| 中文乱码免费一区二区\| 成人激情视频网\| 九九视频在线观看\| 91蝌蚪精品视频\| 欧美视频中文在线看\| 无码免费一区二区三区免费播放\| 最近中文字幕免费观看\| 大胆日韩av\| 日韩亚洲欧美综合\| 免费看国产曰批40分钟\| 日韩精品视频无播放器在线看 \| 国产男女猛烈无遮挡在线喷水\| 网友自拍亚洲\| 亚洲人成影院在线观看\| 国产亚洲精品美女久久久m\| 久久精品视频5\| 精品视频网站\| 欧美大胆一级视频\| 久久久噜噜噜www成人网\| 激情综合闲人网\| 国产精品一区在线\| 日韩av免费在线\| 亚洲国产美女视频\| 老司机精品在线\| 欧美精品电影在线播放\| 男女猛烈激情xx00免费视频\| 欧美zozo\| 成人丝袜高跟foot\| 成人黄在线观看\| 在线免费观看国产精品\| 亚洲一区二区三区\| 亚洲最新中文字幕\| 亚洲永久无码7777kkk\| 精品自拍视频\| 欧美日韩一区二区在线 \| 日本黄色一级网站\| 日韩影院在线\| 亚洲午夜久久久久\| 亚洲小说欧美另类激情\| 神马精品久久\| 成年人国产精品\| 成人亚洲欧美一区二区三区\| 丁香社区五月天\| 欧美日韩一区自拍\| 久久中国妇女中文字幕\| 1024手机在线观看你懂的\| 北条麻妃一区二区三区在线观看 \| 5566成人精品视频免费\| 久草资源在线视频\| 91综合视频\| 日韩中文字幕不卡视频\| 免费看日本黄色片\| 精品国产影院\| 日韩精品免费在线视频\| 国产十八熟妇av成人一区\| 97久久精品一区二区三区的观看方式\| 日韩欧美一区二区在线\| 日本成年人网址\| 操人在线观看\| 亚洲国产一区二区三区\| 97超碰在线人人\| 五月天激情在线\| 亚洲已满18点击进入久久\| 欧美交换配乱吟粗大25p\| 日本电影在线观看网站\| 国产精品久久久久久久蜜臀\| 亚洲一区在线直播\| 欧美男男激情freegay\| 久久先锋影音av\| 日本不卡二区\| 四虎影视精品成人\| 久久久精品蜜桃\| 日韩欧美视频第二区\| 暖暖视频在线免费观看\| 久久精品夜夜夜夜久久\| 色涩成人影视在线播放\| 四虎影院在线域名免费观看\| 国产欧美日韩不卡免费\| 中文字幕在线中文字幕日亚韩一区\| 国产对白叫床清晰在线播放\| 国产精品视频免费\| 一区二区三区电影\| 国产91在线视频蝌蚪\| 一区二区三区欧美久久\| 国产黄页在线观看\| 欧美特黄aaaaaaaa大片\| 欧美精品自拍偷拍动漫精品\| 男人女人拔萝卜视频\| 国产成人av毛片\| 永久免费看mv网站入口亚洲\| 波多野结衣亚洲色图\| 国户精品久久久久久久久久久不卡\| 久久久久国产视频\| 无码人妻精品一区二区\| 青娱乐精品视频在线\| 国产精品99久久久久久久\| 在线看的av\| 国产精品免费av\| 妺妺窝人体色777777\| 电影一区二区三\| 精品少妇一区二区三区在线播放\| 性欧美成人播放77777\| 国产在线日韩精品\| 高清视频欧美一级\| 中文字幕一级片\| 成人免费视频视频\| 一本—道久久a久久精品蜜桃\| 天堂va在线\| 欧美日产国产精品\| 欧洲女同同性吃奶\| 午夜天堂精品久久久久\| 国产免费一区二区三区在线观看\| 婷婷在线观看视频\| 亚洲欧洲色图综合\| 波多野结衣xxxx\| 日韩精品免费一区二区三区竹菊 \| 国产福利一区二区三区在线观看\| 日本人妖在线\| 天涯成人国产亚洲精品一区av\| 婷婷激情小说网\| 国产日产一区\| 日韩av观看网址\| 免费看成年人视频在线观看\| 亚洲人妖av一区二区\| 久久精品国产露脸对白\| 国产伦精品一区二区三区视频\| 2019中文在线观看\| 天天摸天天碰天天爽天天弄\| 亚洲欧洲成人自拍\| 特黄视频免费观看\| 精品久久久久久久久久久下田\| 日本精品视频在线观看\| 中文字幕免费在线观看\| 亚洲福利视频导航\| 亚洲色图14p\| 亚洲二区精品\| 开心色怡人综合网站\| 欧美精品videossex少妇\| 制服.丝袜.亚洲.另类.中文\| 欧产日产国产v\| 精品一区二区三区影院在线午夜 \| 在线精品国产欧美\| 一级特黄性色生活片\| 日韩欧美在线精品\| 青青精品视频播放\| 亚洲一区二区三区成人\| 欧美性xxxxhd\| 婷婷丁香综合网\| 久久er精品视频\| 免费观看亚洲视频\| gogo久久日韩裸体艺术\| 国产91成人video\| 水中色av综合\| 欧美人xxxx\| 国产主播在线播放\| 99精品在线免费\| 国产免费视频传媒\| 久久国产电影\| 激情久久av\| 欧美xoxoxo\| 欧美成人午夜影院\| 九草视频在线观看\| 91成人在线精品\| 亚洲欧美小视频\| 成人三级在线视频\| 国产高潮免费视频\| 五月天久久久\| 鲁片一区二区三区\| 精品日本视频\| 国外成人在线视频\| 韩国精品视频\| 精品福利一区二区三区\| 中文字幕你懂的\| 一区二区三区91\| 亚洲码无人客一区二区三区\| 看片网站欧美日韩\| 亚洲熟妇av日韩熟妇在线\| 成人免费a**址\| 久久av一区二区三区漫画\| 91在线亚洲\| 国产999精品\| 午夜av在线免费观看\| 色噜噜国产精品视频一区二区 \| 成人性生活免费看\| 日本在线不卡视频\| 丰满少妇被猛烈进入高清播放\| 欧美偷拍综合\| 日本高清不卡三区\| 久久综合五月婷婷\| 91在线免费看片\| av在线日韩\| 欧美最猛性xxxx\| 激情网站在线\| 久久视频免费观看\| 国产三级视频在线\| 亚洲精品小视频\| 无码精品一区二区三区在线\| 51精品久久久久久久蜜臀\| 国产精品久久精品视\| 中文字幕第四页\| 一区二区久久久久\| 欧美精品一区二区成人\| 中文字幕不卡的av\| 阿v天堂2014\| 2024国产精品\| 国产又爽又黄无码无遮挡在线观看\| 国产一区二区精品久久91\| 中文字幕1234区\| 奇米一区二区三区\| 视频在线观看免费高清\| 日韩国产欧美在线观看\| 四季av一区二区\| 久久国产精品99国产\| 国产性生交xxxxx免费\| 亚洲专区一区\| 五月婷婷激情久久\| 天堂精品中文字幕在线\| 日本特黄a级片\| 蜜臀av性久久久久蜜臀aⅴ流畅\| 91在线视频观看免费\| 爽好久久久欧美精品\| 国产永久免费网站\| 精品亚洲国产成人av制服丝袜\| 免费在线观看污网站\| 久久国产福利国产秒拍\| 人妻精品久久久久中文字幕69\| 国产伦精品一区二区三区免费 \| 亚洲国产aⅴ精品一区二区三区\| 成人福利免费观看\| 精品午夜视频\| 久久伦理网站\|

練習(xí)冊(cè)

高中

初中

小學(xué)