
題目列表(包括答案和解析)
A、
| ||
B、
| ||
C、
| ||
D、
|
A.
| B.
| C.
| D.
|
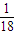


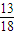
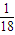


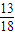




1-5 DCACC 6-10 ABACA
11.1或-3 12.12 13.  14.15 15.
14.15 15.
16.解:因為
所以 
故  …………6分
…………6分
令 ,則
,則 的單調遞增的正值區間是
的單調遞增的正值區間是
 ,
,
單調遞減的正值區間是
當 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為
當 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為 (注:區間為開的不扣分)…………12分
(注:區間為開的不扣分)…………12分
17.(本題滿分12分)
解:(Ⅰ)記“該學生恰好經過4次測試考上大學”的事件為事件A,則 ……6分
……6分
(Ⅱ)記“該生考上大學”的事件為事件B,其對立事件為 ,則
,則 ∴
∴ ……12分
……12分
18.解:(1)當M為PC的中點時,PC⊥平面MDB.------------------1分
事實上,連BM,DM,取AD的中點N,連NB,NP.
因為 ,且平面PAD
,且平面PAD 平面ABCD,所以PN⊥平面ABCD.
平面ABCD,所以PN⊥平面ABCD.
在 中,
中, ,所以
,所以 ,又
,又
所以 ,又
,又 ,
, 平面MDB,
平面MDB,
而PD=DC=2,所以 ,所以
,所以 平面MDB------------------6分
平面MDB------------------6分
(2)易知G在中線BM上,過M作 于F,連CF,
于F,連CF,
因為 平面MDB,所以
平面MDB,所以 ,
,
故 是二面角G―BD―C的平面角
------------------9分
是二面角G―BD―C的平面角
------------------9分
在 中,
中, ,所以
,所以 ,又
,又
所以 ,故二面角G―BD―C的大小為
,故二面角G―BD―C的大小為 ----------------12分
----------------12分
19.21.解:(1)三個函數的最小值依次為 ,
, ,
,
由 ,得
,得
∴
 ,
,
故方程 的兩根是
的兩根是 ,
, .
.
故 ,
, .
.
 ,即
,即
∴  .………………6分
.………………6分
(2)①依題意 是方程
是方程 的根,
的根,
故有 ,
, ,
,
且△ ,得
,得 .
.
由 ……………9分
……………9分

 ;得,
;得, ,
, .
.
由(1)知 ,故
,故 ,
,
∴
 ,
,
∴
 .………………………12分
.………………………12分
20.(1)解法一:設 ,
, ,
, ,則
,則
 兩式相減,得:
兩式相減,得: 
又  ,
, ,
, ,
,
可得
 ……………………………………(5分)
……………………………………(5分)
解法二:設 ,
, ,
, ,,直線
,,直線 ①
①



 ,
, 
 ,又
,又

由條件:
即 ……………………………………………………………………(5分)
……………………………………………………………………(5分)
(2)由①及 ,可知
,可知 代入橢圓方程,得
代入橢圓方程,得
 ………………………………………………………………………(10分)
………………………………………………………………………(10分)
又



 …………………………………………………(13分)
…………………………………………………(13分)
21.解: (Ⅰ)依題意有 ,于是
,于是 .
.
所以數列 是等差數列.
………………….2分
是等差數列.
………………….2分
(Ⅱ)由題意得 ,即
,即 , (
, ( )
①
)
①
所以又有 .
② ………4分
.
② ………4分
由② ①得
①得 ,
,
可知 都是等差數列.那么得
都是等差數列.那么得
 ,
,
 . (
. (


故 …………8分
…………8分
(Ⅲ)當 為奇數時,
為奇數時, ,所以
,所以
當 為偶數時,
為偶數時, 所以
所以
作 軸,垂足為
軸,垂足為 則
則 ,要使等腰三角形
,要使等腰三角形 為直角三角形,必須且只需
為直角三角形,必須且只需 .
.
當 為奇數時,有
為奇數時,有 ,即
,即 .
①
.
①
當 時,
時, ;當
;當 時,
時, ;當
;當 , ①式無解.
, ①式無解.
當 為偶數時,有
為偶數時,有 ,同理可求得
,同理可求得 .
.
綜上所述,上述等腰三角形 中存在直角三角形,此時
中存在直角三角形,此時 的值為
的值為 或
或
或 .
……………………..14分
.
……………………..14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com