
題目列表(包括答案和解析)
y 社區數量 x |
居民素質 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
| 社 區 服 務 |
1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | a | b | 6 | 0 | 1 | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
| 167 |
| 50 |
在四棱錐 中,
中, 平面
平面 ,底面
,底面 為矩形,
為矩形, .
.
(Ⅰ)當 時,求證:
時,求證: ;
;
(Ⅱ)若 邊上有且只有一個點
邊上有且只有一個點 ,使得
,使得 ,求此時二面角
,求此時二面角 的余弦值.
的余弦值.

【解析】第一位女利用線面垂直的判定定理和性質定理得到。當a=1時,底面ABCD為正方形,

又因為 ,
, ………………2分
………………2分
又 ,得證。
,得證。
第二問,建立空間直角坐標系,則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
設BQ=m,則Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 時,存在點Q使得
時,存在點Q使得
當且僅當m=a-m,即m=a/2時,BC邊上有且只有一個點Q,使得
由此知道a=2, 設平面POQ的法向量為
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
則 的大小與二面角A-PD-Q的大小相等所以
的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
解:(Ⅰ)當 時,底面ABCD為正方形,
時,底面ABCD為正方形,

又因為 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因為AB,AD,AP兩兩垂直,分別以它們所在直線為X軸、Y軸、Z軸建立坐標系,如圖所示,

則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
設BQ=m,則Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 時,存在點Q使得
時,存在點Q使得
當且僅當m=a-m,即m=a/2時,BC邊上有且只有一個點Q,使得 由此知道a=2,
由此知道a=2,
設平面POQ的法向量為
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
則 的大小與二面角A-PD-Q的大小相等所以
的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
(本題滿分12分)某電信部門執行的新的電話收費標準中,其中本地網營業區內的通話費標準:前3分鐘為0.20元(不足3分鐘按3分鐘計算),以后的每分鐘收0.10元(不足1分鐘按1分鐘計算。)在一次實習作業中,某同學調查了A、B、C、D、E五人某天撥打的本地網營業區內的電話通話時間情況,其原始數據如下表所示:
| A | B | C | D | E | |
| 第一次通話時間 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通話時間 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通話時間 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 應繳話費(元) |
⑴在上表中填寫出各人應繳的話費;
⑵設通話時間為t分鐘,試根據上表完成下表的填寫(即這五人在這一天內的通話情況統計表):
| 時間段 | 頻數累計 | 頻數 | 頻率 | 累計頻率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | ||||
| 4<t≤5 | ||||
| 5<t≤6 | ||||
| 合計 | 正 正 |
⑶若該本地網營業區原來執行的電話收費標準是:每3分鐘為0.20元(不足3分鐘按3分鐘計算)。問這五人這天的實際平均通話費與原通話標準下算出的平均通話費相比,是增多了還是減少了?增或減了多少?
(文)某電信部門執行的新的電話收費標準中,其中本地網營業區內的通話費標準:前3分鐘為0.20元(不足3分鐘按3分鐘計算),以后的每分鐘收0.10元(不足1分鐘按1分鐘計算。)在一次實習作業中,某同學調查了A、B、C、D、E五人某天撥打的本地網營業區內的電話通話時間情況,其原始數據如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通話時間 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通話時間 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通話時間 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
應繳話費(元) |
|
|
|
|
|
(1)在上表中填寫出各人應繳的話費;
(2)設通話時間為t分鐘,試根據上表完成下表的填寫(即這五人在這一天內的通話情況統計表):
|
時間段 |
頻數累計 |
頻數 |
頻率 |
累計頻率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合計 |
正 正 |
|
|
|
(3)若該本地網營業區原來執行的電話收費標準是:每3分鐘為0.20元(不足3分鐘按3分鐘計算)。問這五人這天的實際平均通話費與原通話標準下算出的平均通話費相比,是增多了還是減少了?增或減了多少?
如圖所示的長方體 中,底面
中,底面 是邊長為
是邊長為 的正方形,
的正方形, 為
為 與
與 的交點,
的交點, ,
, 是線段
是線段 的中點.
的中點.
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本試題主要考查了線面平行的判定定理和線面垂直的判定定理,以及二面角的求解的運用。中利用 ,又
,又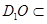 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得證明
.
可得證明
(3)因為∴ 為面
為面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 為平面
為平面 的法向量.∴利用法向量的夾角公式,
的法向量.∴利用法向量的夾角公式, ,
,
∴ 與
與 的夾角為
的夾角為 ,即二面角
,即二面角 的大小為
的大小為 .
.
方法一:解:(Ⅰ)建立如圖所示的空間直角坐標系.連接 ,則點
,則點 、
、 ,
,

∴ ,又點
,又點 ,
, ,∴
,∴
∴ ,且
,且 與
與 不共線,∴
不共線,∴ .
.
又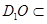 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 為面
為面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 為平面
為平面 的法向量.∴
的法向量.∴ ,
,
∴ 與
與 的夾角為
的夾角為 ,即二面角
,即二面角 的大小為
的大小為
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com