日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

查看答案和解析>>

查看答案和解析>>

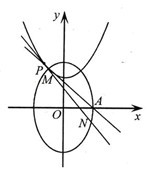
（本題滿分15分）如圖△ABC為直角三角形，點(diǎn)M在y軸上，且，點(diǎn)C在x軸上移動(dòng)， （I）求點(diǎn)B的軌跡E的方程；（II）過(guò)點(diǎn)的直線l與曲線E交于P、Q兩點(diǎn)，

設(shè)的夾角為

的取值范圍；   （III）設(shè)以點(diǎn)N(0，m)為圓心，以為

半徑的圓與曲線E在第一象限的交點(diǎn)H，若圓在點(diǎn)H處的

切線與曲線E在點(diǎn)H處的切線互相垂直，求實(shí)數(shù)m的值。

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

1、  2、充分不必要；3、；4、73；5、8；6、5049；

7、1；8、；9、；10、；11、圓內(nèi)；12、；

13、；14、

15、解：（Ⅰ）設(shè)區(qū)域A中任意一點(diǎn)P為事件M．?????????????????????????????????????? 1分

因?yàn)閰^(qū)域A的面積為，區(qū)域B在區(qū)域A的面積為，????????????????????? 5分

故．??????????????????????????????????????????????????????????????????????????????????????????? 7分

（Ⅱ）設(shè)點(diǎn)P在集合B為事件N，????????????????????????????????????????????????????????????? 8分

甲、乙兩人各擲一次骰子所得的點(diǎn)P的個(gè)數(shù)為36個(gè)，其中在區(qū)域B中的點(diǎn)P有21個(gè)．    12分

故．

16、解：（1）因?yàn)?sub>邊所在直線的方程為，且與垂直，所以直線的斜率為．………………………………………3分

又因?yàn)辄c(diǎn)在直線上，所以邊所在直線的方程為即．   ………………………………………7分

（2）由解得點(diǎn)的坐標(biāo)為，因?yàn)榫匦?sub>兩條對(duì)角線的交點(diǎn)為．所以為矩形外接圓的圓心．又．從而矩形外接圓的方程為．…………………………………14分

17、證明：（Ⅰ）在中，

∵，，，∴．

∴．----------------2分

又 ∵平面平面，

平面平面，平面，∴平面．

又平面，∴平面平面．----------4分

（Ⅱ）當(dāng)點(diǎn)位于線段PC靠近C點(diǎn)的三等分點(diǎn)

  處時(shí)，平面．--------5分

證明如下：連接AC，交于點(diǎn)N，連接MN．

∵，所以四邊形是梯形．

∵，∴．

又 ∵，

∴，∴MN．????????????????????????????????????????????????????????????? 7分

∵平面，∴平面．??????????????????????????????????????????????????????? 9分

（Ⅲ）過(guò)作交于，

∵平面平面，

∴平面．

即為四棱錐的高．??????????????????????????????????????????????????????????????????? 11分

又 ∵是邊長(zhǎng)為4的等邊三角形，∴．??????????????????? 12分

在中，斜邊邊上的高為，此即為梯形的高．

∴梯形的面積．????????????????????????????????????????? 14分

故．   

18、解：（1）由，得

，…………………………2分

，

， ，

于是， ，

∴，即．…………………………7分

（2）∵角是一個(gè)三角形的最小內(nèi)角，∴0<≤,,………………10分

設(shè),則≥（當(dāng)且僅當(dāng)時(shí)取=）,………12分

故函數(shù)的值域?yàn)?sub>．…

19、解：（1）2008年A型車價(jià)格為32+32×25%=40（萬(wàn)元）

設(shè)B型車每年下降d萬(wàn)元，2003，2003，…，2008年B型車價(jià)格分別為…，為公差是－d的等差數(shù)列）

即

故每年至少下降2萬(wàn)元。

（2）2008年到期時(shí)共有錢33

（萬(wàn)元）

故5年到期后這筆錢夠買一輛降價(jià)后的B型車。

20、（I）由已知，可得，，1分                                       

∴ 解之得，                    3分

                      4分  

（II）          5分

=  8分

（III）

               10分

          （1）

      （2）

（1）―（2）得：

=，即，當(dāng)時(shí)， ，13分

，使得當(dāng)時(shí)，恒成立     14分