
題目列表(包括答案和解析)
| 分數段 | [29~40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 午休考生 人數 |
23 | 47 | 30 | 21 | 14 | 31 | 14 |
| 不午休考 生人數 |
17 | 51 | 67 | 15 | 30 | 17 | 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 及格人數 | 不及格人數 | 總計 | |
| 午休 | |||
| 不午休 | |||
| 總計 |
20.在二項式 的展開式中,前三項系數的絕對值成等差數列
的展開式中,前三項系數的絕對值成等差數列
(1)求展開式的常數項; (2)求展開式中二項式系數最大的項;
(3)求展開式中各項的系數和。
【解析】本試題主要考查了二項式定理中通項公式和二項式系數的概念以及求解各個系數和的運用,賦值法思想要深刻體會。
(本題滿分12分)已知函數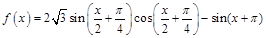 。
。
(1)求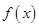 的最小正周期;
的最小正周期;
(2)若將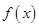 的圖象向右平移
的圖象向右平移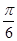 個單位,得到函數
個單位,得到函數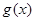 的圖象,求函數
的圖象,求函數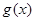 在區間
在區間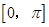 上的最大值和最小值。
上的最大值和最小值。
【解析】第一問中主要利用三角函數的兩角和差公式化簡為單一三角函數解析式
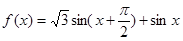 =
=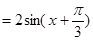
然后利用周期公式得到第一問。
第二問中,由于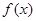 的圖象向右平移
的圖象向右平移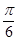 個單位,得到函數
個單位,得到函數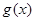 的圖象,
的圖象,
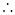
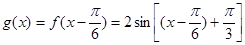
然后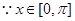 時,
時,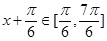 結合三角函數值域求解得到范圍。
結合三角函數值域求解得到范圍。
已知在△ABC中,角A、B、C所對的邊分別為a,b,c,且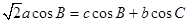 。
。
(1)求角B的大小;
(2)設向量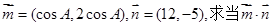 取最大值時,tanC的值。
取最大值時,tanC的值。
【解析】本試題主要是考查了解三角形中正弦定理的運用,先求解B,然后,利用數量積公式我們表示向量積,從而借助于三角形中值域來求解C的正切值。
在△ABC中,角A,B,C所對的邊分別為a,b,c, △ABC的面積
S=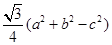
(1)求角C的大小
(2)若c=1,求△ABC周長L的取值范圍
【解析】本試題主要是考查了解三角形中的面積公式和兩個定理的運用。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com