
題目列表(包括答案和解析)
設數列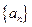 的前
的前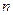 項和為
項和為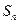 ,點
,點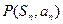 在直線
在直線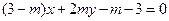 上,
上,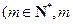 為常數,
為常數,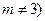 .
.
(Ⅰ)求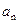 ;
;
(Ⅱ)若數列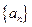 的公比
的公比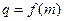 ,數列
,數列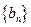 滿足
滿足 ,求證:
,求證: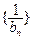 為等差數列,并求
為等差數列,并求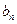 ;
;
(III)設數列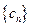 滿足
滿足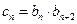 ,
,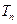 為數列
為數列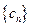 的前
的前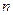 項和,且存在實數
項和,且存在實數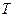 滿足
滿足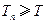 ,
,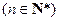 ,求
,求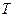 的最大值.
的最大值.
設數列 的前
的前 項和為
項和為 ,點
,點 在直線
在直線 上,
上, 為常數,
為常數, .
.
(Ⅰ)求 ;
;
(Ⅱ)若數列 的公比
的公比 ,數列
,數列 滿足
滿足 ,求證:
,求證: 為等差數列,并求
為等差數列,并求 ;
;
(III)設數列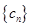 滿足
滿足 ,
, 為數列
為數列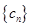 的前
的前 項和,且存在實數
項和,且存在實數 滿足
滿足 ,
, ,求
,求 的最大值.
的最大值.
設數列 的前
的前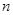 項和為
項和為 ,點
,點 在直線
在直線 上,
上, 為常數,
為常數, .
.
(Ⅰ)求 ;
;
(Ⅱ)若數列 的公比
的公比 ,數列
,數列 滿足
滿足 ,求證:
,求證: 為等差數列,并求
為等差數列,并求 ;
;
(III)設數列 滿足
滿足 ,
, 為數列
為數列 的前
的前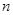 項和,且存在實數
項和,且存在實數 滿足
滿足 ,
, ,求
,求 的最大值.
的最大值.
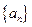 的前
的前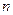 項和為
項和為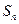 ,點
,點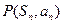 在直線
在直線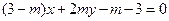 上,
上,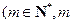 為常數,
為常數,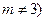 .
.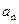 ;
;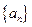 的公比
的公比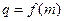 ,數列
,數列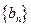 滿足
滿足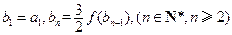 ,求證:
,求證: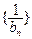 為等差數列,并求
為等差數列,并求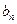 ;
;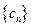 滿足
滿足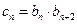 ,
,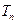 為數列
為數列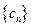 的前
的前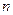 項和,且存在實數
項和,且存在實數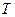 滿足
滿足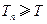 ,
,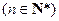 ,求
,求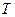 的最大值.
的最大值.已知數列![]()
![]() 的前
的前![]()
![]() 項和為
項和為![]()
![]() ,通項為
,通項為![]()
![]() ,且滿足
,且滿足![]()
![]() (
(![]()
![]() 是常數且
是常數且![]()
![]() ).
).
(I)求數列![]()
![]() 的通項公式;
的通項公式;
(II) 當![]()
![]() 時,試證明
時,試證明![]()
![]() ;
;
(III)設函數![]()
![]() ,
,![]()
![]() ,是否存在正整數
,是否存在正整數![]()
![]() ,使
,使![]()
![]() 對
對![]()
![]() 都成立?若存在,求出
都成立?若存在,求出![]()
![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
1.D 2.C 3.A 4.B 5.A 6.B 7.B 8.D 9.C 10.B
11.A 12.B
13. 14.
14.  15.
15.  16.
16.
17.(本小題滿分12分)
(Ⅰ)由正弦定理知sinA= ,sinB
,sinB ,sinC=
,sinC= .
.
∴ 2
 ,
,
∴  .
.
∴ ,
, .
.
(Ⅱ)∵  =
=
= =
= =
=
= =
= .
.
 ,∴
,∴ ,
,
∴當 時,即
時,即 時
時 .
.
18.(本小題滿分12分)
解(1)記得分之和為隨機變量
則 =0,1,2 其中
=0,1,2 其中



0
1
2
P




(2)
19、(本小題滿分12分)
(I)解:由 得
得
 ,
,

(II)由 ,
,
∴數列{ }是以S1+1=2為首項,以2為公比的等比數列,
}是以S1+1=2為首項,以2為公比的等比數列,

 當n=1時a1=1滿足
當n=1時a1=1滿足
(III) ①
①
 ,②
,②
①-②得 ,
,
則 .
.
20、(本小題滿分12分)
解:
(Ⅰ)∵ .
.
∴當 時,
時, .
.
因為, 對一切
對一切 成立,
成立,
所以, 對一切
對一切 成立,所以
成立,所以 是R上的減函數,
是R上的減函數,
因此, 沒有極值.
沒有極值.
(Ⅱ)∵ 是R上的增函數,故
是R上的增函數,故 在R上恒成立,
在R上恒成立,
即 在R上恒成立.
在R上恒成立.
令 ,可得,
,可得,
 .
.
由 ,得
,得 或
或 .
.
因此,函數 在
在 上單調遞減,在(-1,1)上單調遞增,
上單調遞減,在(-1,1)上單調遞增,
在(1,+ )上單調遞減.
)上單調遞減.
∴當 時,
時, 有極小值
有極小值 ,當
,當 時,
時, 有極大值
有極大值 .
.
又 ,故知
,故知 為函數
為函數 的最小值.
的最小值.
∴ ,但是當
,但是當 時,
時, 也是R上的增函數.
也是R上的增函數.
因此a的取值范圍是 .
.
21、(本小題滿分12分)
解:(1)由橢圓定義及已知條件知
又c=4,∴b2=a2-c2=9.
故橢圓方程為 +
+ =1.
=1.
(2)由點B在橢圓上,可知|F2B|=|yB|= ,而橢圓的右準線方程為x=
,而橢圓的右準線方程為x= ,離心率為
,離心率為 ,
,
由橢圓定義有|F2A|= (
( -x1),|F2C|=
-x1),|F2C|= (
( -x2).
-x2).
依題意|F2A|+|F2C|=2|F2B|.
則 (
( -x1)+
-x1)+ (
( -x2)=2×
-x2)=2× .
.
∴x1+x2=8.
設弦AC的中點為P(x0,y0),則x0= =4,
=4,
即弦AC的中點的橫坐標為4.
(3)由A(x1,y1),C(x2,y2)在橢圓上得9x12+25y12=9×25,9x22+25y22=9×25.
兩式相減整理得9( )+25(
)+25( )(
)( )=0(x1≠x2).
)=0(x1≠x2).
將 =x0=4,
=x0=4, =y0,
=y0, =-
=- (k≠0)代入得
(k≠0)代入得
9×4+25y0(- )=0,即k=
)=0,即k= y0.
y0.
由于P(4,y0)在弦AC的垂直平分線上,
∴y0=4k+m,于是m=y0-4k=y0- y0=-
y0=- y0.
y0.
而- <y0<
<y0< ,∴-
,∴- <m<
<m< .
.
22、(本小題滿分12分)
解:(I)① 時,
時, ,
,
故結論成立.
②假設 時結論成立,即
時結論成立,即 .
.
∴ ,即
,即 .
.
也就是說 時,結論也成立.
時,結論也成立.
由①②可知,對一切 均有
均有 .
.
(Ⅱ)要證 ,即證
,即證 ,其中
,其中 .
.
令 ,
, .
.
由 ,得
,得 .
.





+
0
―


極大值

又 ,
, .
.
∴當 ,
, ,∴
,∴ .
.
∴ ,即
,即 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com