日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

【題目】（題文）（題文）已知橢圓的離心率為,過右焦點且斜率為1的直線交橢圓于A,B兩點, N為弦AB的中點,O為坐標原點.

(1)求直線ON的斜率；

(2)求證:對于橢圓上的任意一點M,都存在,使得成立.

【題目】已知曲線C的極坐標方程是.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數方程是: 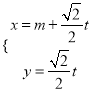(是參數).

(Ⅰ)將曲線C的極坐標方程化為直角坐標方程,將直線的參數方程化為普通方程;

(Ⅱ)若直線l與曲線C相交于A、B兩點,且,試求實數m的值.

【題目】已知函數．

（1）求函數的極值；

（2）對于曲線上的不同兩點，如果存在曲線上的點，且使得曲線在點處的切線，則稱為弦的伴隨直線，特別地，當時，又稱為的—伴隨直線．

①求證：曲線的任意一條弦均有伴隨直線，并且伴隨直線是唯一的；

②是否存在曲線，使得曲線的任意一條弦均有—伴隨直線？若存在，給出一條這樣的曲線，并證明你的結論；若不存在，說明理由．

【題目】直線ax＋by＝1與圓x2＋y2＝1相交于A，B兩點(其中a，b是實數)，且△AOB是直角三角形(O是坐標原點)，則點P(a，b)與點(0,1)之間距離的最小值為( )．

A.0B.C.－1D.＋1

【題目】如圖a是某市參加2012年高考的學生身高條形統計圖，從左到右的各條形表示的學生人數依次記為、、…、[如表示身高（單位：cm）在內的學生人數]．圖b是統計圖a中身高在一定范圍內學生人數的一個算法流程圖．現要統計身高在（含160cm，不含180cm）的學生人數，那么在流程圖中的判斷框內應填寫的條件是（ ）

A.B.C.D.

【題目】《數書九章》是中國南宋時期杰出數學家秦九韶的著作，全書十八卷共八十一個問題，分為九類，每類九個問題，《數書九章》中記錄了秦九昭的許多創造性成就，其中在卷五“三斜求積”中提出了已知三角形三邊，，求面積的公式，這與古希臘的海倫公式完成等價，其求法是:“以小斜冪并大斜冪減中斜冪，余半之，自乘于上，以小斜冪乘大斜冪減上，余四約之，為實，一為從隅，開平方得積.”若把以上這段文字寫成公式，即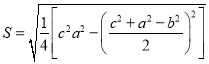.現有滿足，且的面積，請運用上述公式判斷下列命題正確的是

A.周長為

B.三個內角，，成等差數列

C.外接圓直徑為

D.中線的長為

【題目】設函數，.

（1）若，求函數的單調區間；

（2）若，且函數在區間內有兩個極值點，求實數a的取值范圍；

（3）求證：對任意的正數a，都存在實數t，滿足：對任意的，.

【題目】已知數列滿足：（常數），（，）.數列滿足：（）.

（1）求，的值；

（2）求數列的通項公式；

（3）是否存在k，使得數列的每一項均為整數？若存在，求出k的所有可能值；若不存在，請說明理由.

【題目】如圖，，是某景區的兩條道路（寬度忽略不計，為東西方向），Q為景區內一景點，A為道路上一游客休息區，已知，（百米），Q到直線，的距離分別為3（百米），（百米），現新修一條自A經過Q的有軌觀光直路并延伸至道路于點B，并在B處修建一游客休息區.

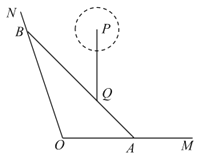
（1）求有軌觀光直路的長；

（2）已知在景點Q的正北方6百米的P處有一大型組合音樂噴泉，噴泉表演一次的時長為9分鐘，表演時，噴泉噴灑區域以P為圓心，r為半徑變化，且t分鐘時，（百米）（，）.當噴泉表演開始時，一觀光車S（大小忽略不計）正從休息區B沿（1）中的軌道以（百米/分鐘）的速度開往休息區A，問：觀光車在行駛途中是否會被噴泉噴灑到，并說明理由.

【題目】在平面直角坐標系中，已知橢圓E：（）過點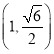，其心率等于.

（1）求橢圓E的標準方程；

（2）若A，B分別是橢圓E的左，右頂點，動點M滿足，且橢圓E于點P.

①求證：為定值：

②設與以為直徑的圓的另一交點為Q，求證：直線經過定點.