
【題目】(題文)(題文)已知橢圓![]() 的離心率為
的離心率為![]() ,過右焦點
,過右焦點![]() 且斜率為1的直線交橢圓
且斜率為1的直線交橢圓![]() 于A,B兩點, N為弦AB的中點,O為坐標原點.
于A,B兩點, N為弦AB的中點,O為坐標原點.
(1)求直線ON的斜率![]() ;
;
(2)求證:對于橢圓![]() 上的任意一點M,都存在
上的任意一點M,都存在![]() ,使得
,使得![]() 成立.
成立.
【答案】(1) ![]() .
.
(2)見解析.
【解析】分析:(1)設橢圓的焦距為![]() ,由
,由![]() ,可得
,可得![]() ,從而橢圓
,從而橢圓![]() 的方程可化為
的方程可化為![]() ,右焦點
,右焦點![]() ,直線
,直線![]() 所在的直線方程為
所在的直線方程為![]() ,與橢圓方程聯立化為
,與橢圓方程聯立化為![]() ,在利用中點公式與斜率公式即可求出;
,在利用中點公式與斜率公式即可求出;
(2)利用平面向量的基本定理,根與系數的關系,點與橢圓的位置關系,即可得到證明.
詳解: (1)設橢圓的焦距為![]() ,因為
,因為![]() ,所以有
,所以有![]() ,故有
,故有![]() .
.
從而橢圓![]() 的方程可化為:
的方程可化為:![]()
知右焦點![]() 的坐標為(
的坐標為(![]() ),據題意有
),據題意有![]() 所在的直線方程為:
所在的直線方程為:![]() . ②由①,②有:
. ②由①,②有:![]() .
.
③設![]() ,弦
,弦![]() 的中點
的中點![]() ,由③及韋達定理有:
,由③及韋達定理有:
![]()
所以![]() ,即為所求.
,即為所求.
(2)顯然![]() 與
與![]() 可作為平面向量的一組基底,由平面向量基本定理,對于這一平面內的向量
可作為平面向量的一組基底,由平面向量基本定理,對于這一平面內的向量![]() ,有且只有一對實數
,有且只有一對實數![]() ,使得等式
,使得等式![]() 成立.設
成立.設![]() ,由(1)中各點的坐標有:
,由(1)中各點的坐標有:![]() ,故
,故![]() .
.
又因為點![]() 在橢圓
在橢圓![]() 上,所以有
上,所以有![]() 整理可得:
整理可得:
![]() . ④
. ④
由③有:![]() .所以
.所以
![]() ⑤又點
⑤又點![]() 在橢圓
在橢圓![]() 上,故有
上,故有![]() .
.
⑥將⑤,⑥代入④可得:![]() .
.
所以,對于橢圓上的每一個點![]() ,總存在一對實數,使等式
,總存在一對實數,使等式![]() 成立,且
成立,且![]() .
.
所以存在![]() ,使得
,使得![]() .也就是:對于橢圓
.也就是:對于橢圓![]() 上任意一點
上任意一點![]() ,總存在
,總存在![]() ,使得等式
,使得等式![]() 成立.
成立.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】從你所在班級任意選出6名同學,調查他們的出生月份,假設出生在一月,二月……十二月是等可能的.設事件![]() “至少有兩人出生月份相同”,設計一種試驗方法,模擬20次,估計事件
“至少有兩人出生月份相同”,設計一種試驗方法,模擬20次,估計事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓C過定點F(2,0),且與直線x=-2相切,圓心C的軌跡為E,
(1)求圓心C的軌跡E的方程;
(2)若直線l交E與P,Q兩點,且線段PQ的中心點坐標(1,1),求|PQ|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為一個摩天輪示意圖。該摩天輪圓半徑為4.8m,圓上最低點與地面距離為0.8m,60s轉動一周.圖中OA與地面垂直。以O為始邊,逆時針轉動0角到OB設B點與地面的距離為hm.

(1)求h與![]() 的函數解析式;
的函數解析式;
(2)設從OA開始轉動,經過ts到達OB,求h與t的函數解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若f (x)在區間(-∞,2)上為單調遞增函數,求實數a的取值范圍;
(2)若a=0,x0<1,設直線y=g(x)為函數f (x)的圖象在x=x0處的切線,求證:f (x)≤g(x).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,沒售出1噸該商品可獲利潤0.5萬元,未售出的商品,每1噸虧損0.3萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了130噸該商品,現以![]() (單位:噸,
(單位:噸,![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量,![]() (單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
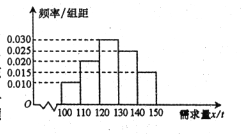
(Ⅰ)視![]() 分布在各區間內的頻率為相應的概率,求
分布在各區間內的頻率為相應的概率,求![]() ;
;
(Ⅱ)將![]() 表示為
表示為![]() 的函數,求出該函數表達式;
的函數,求出該函數表達式;
(Ⅲ)在頻率分布直方圖的市場需求量分組中,以各組的區間中點值(組中值)代表該組的各個值,并以市場需求量落入該區間的頻率作為市場需求量取該組中值的概率(例如![]() ,則取
,則取![]() 的概率等于市場需求量落入
的概率等于市場需求量落入![]() 的頻率),求
的頻率),求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李明自主創業,在網上經營一家水果店,銷售的水果中有草莓、京白梨、西瓜、桃,價格依次為60元/盒、65元/盒、80元/盒、90元/盒.為增加銷量,李明對這四種水果進行促銷:一次購買水果的總價達到120元,顧客就少付x元.每筆訂單顧客網上支付成功后,李明會得到支付款的80%.
①當x=10時,顧客一次購買草莓和西瓜各1盒,需要支付__________元;
②在促銷活動中,為保證李明每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com