日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

方案一：

從抽獎箱中，一次性摸出3個球，其中獎規則為：若摸到3個紅球，享受免單優惠；若摸出2個紅球則打6折，若摸出1個紅球，則打7折；若沒摸出紅球，則不打折.

方案二：

從抽獎箱中，有放回每次摸取1球，連摸3次，每摸到1次紅球，立減200元.每次摸取1球，連摸3次，每摸到1次

（1）若小南、小開均分別消費了600元，且均選擇抽獎方案一，試求他們均享受免單優惠的概率；

（2）若小杰消費恰好滿1000元，試比較說明小杰選擇哪一種抽獎方案更合算？

【題目】已知四棱錐中， 平面，底面為菱形， ， 是中點， 是的中點， 是上的點．

（Ⅰ）求證：平面平面；

（Ⅱ）當是中點，且時，求二面角的余弦值．

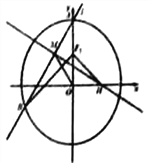
【題目】如圖，在直角坐標系中，橢圓的上焦點為，橢圓的離心率為，且過點.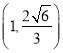

（1）求橢圓的方程.

（2）設過橢圓的上頂點的直線與橢圓交于點（不在軸上），垂直于的直線與交于點，與軸交于點，若，且，求直線的方程.

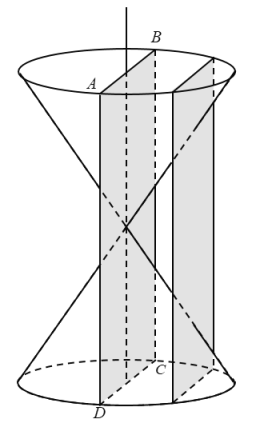
【題目】古希臘數學家阿波羅尼奧斯在他的著作《圓錐曲線論》中記載了用平面切制圓錐得到圓錐曲線的方法.如圖，將兩個完全相同的圓錐對頂放置（兩圓錐的軸重合），已知兩個圓錐的底面半徑為1，母線長均為，記過圓錐軸的平面ABCD為平面（與兩個圓錐面的交線為AC、BD），用平行于的平面截圓錐，該平面與兩個圓錐側面的截線即為雙曲線E的一部分，且雙曲線E的兩條漸近線分別平行于AC、BD，則雙曲線E的離心率為（ ）

A.B.C.D.2

【題目】已知動點P到點的距離與它到直線l：的距離d的比值為，設動點P形成的軌跡為曲線C.

（Ⅰ）求曲線C的方程；

（Ⅱ）過點的直線與曲線C交于A，B兩點，設，，過A點作，垂足為，過B點作，垂足為，求的取值范圍.

【題目】長方體中，F是AB的中點，直線平面，.

（Ⅰ）求長方體的體積；

（Ⅱ）求二面角的余弦值的大小.

【題目】為慶祝建國70周年，校園文化節舉行有獎答題活動，現有A，B兩種題型，從A類題型中抽取1道，從B類題型中抽取2道回答，答對3道題獲新華書店面值為15元的圖書代金券，答對2道題獲面值為10元的圖書代金券，答對1道題獲面值為5元的圖書代金券，沒有答對獲面值為1元的圖書代金券（作為鼓勵）.甲同學參加此活動答對A類題的概率為，答對B類題的概率為.

（Ⅰ）求甲答對1道題的概率；

（Ⅱ）設甲參加一次活動所獲圖書代金券的面值為隨機變量X，求X的分布列和數學期望.

【題目】已知函數.

（Ⅰ）討論的單調性，并證明有且僅有兩個零點；

（Ⅱ）設是的一個零點，證明曲線在點處的切線也是曲線的切線.

【題目】在平面直角坐標系中，曲線的參數方程為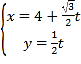（為參數）.以坐標原點為極點,軸正半軸為極軸建立極坐標系,曲線的極坐標方程為

（1）在曲線上任取一點,連接,在射線上取一點，使,求點軌跡的極坐標方程；

（2）在曲線上任取一點,在曲線上任取一點,求的最小值.