
科目: 來源: 題型:
【題目】某花店每天以每枝5元的價格從農場購進若干枝玫瑰花,然后以每枝10元的價格出售.如果當天賣不完,剩下的玫瑰花做垃圾處理.
(Ⅰ)若花店一天購進17枝玫瑰花,求當天的利潤y(單位:元)關于當天需求量n(單位:枝,n∈N)的函數解析式.
(Ⅱ)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(i)假設花店在這100天內每天購進17枝玫瑰花,求這100天的日利潤(單位:元)的平均數;
(ii)若花店一天購進17枝玫瑰花,以100天記錄的各需求量的頻率作為各需求量發生的概率,求當天的利潤不少于75元的概率.
(命題意圖)本題主要考查給出樣本頻數分別表求樣本的均值、將頻率做概率求互斥事件的和概率,是簡單題.
查看答案和解析>>
科目: 來源: 題型:
【題目】國際上通常用年齡中位數指標作為劃分國家或地區人口年齡構成的標準:年齡中位數在20歲以下為“年輕型”人口;年齡中位數在20~30歲為“成年型”人口;年齡中位數在30歲以上為“老齡型”人口.

如圖反映了我國全面放開二孩政策對我國人口年齡中位數的影響.據此,對我國人口年齡構成的類型做出如下判斷:①建國以來直至2000年為“成年型”人口;②從2010年至2020年為“老齡型”人口;③放開二孩政策之后我國仍為“老齡型”人口.其中正確的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 經過橢圓
經過橢圓![]() 的左,右焦點
的左,右焦點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 的垂直平分線與
的垂直平分線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得
,使得![]() 的面積與
的面積與![]() (
(![]() 為原點)的面積相等?若存在,求出
為原點)的面積相等?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】采購經理指數(PMI)是衡量一個國家制造業的“體檢表”,是衡量制造業在生產新訂單、商品價格、存貨、雇員、訂單交貨、新出口訂單和進口等八個方面狀況的指數,下圖為2018年9月—2019年9月我國制造業的采購經理指數(單位:%).
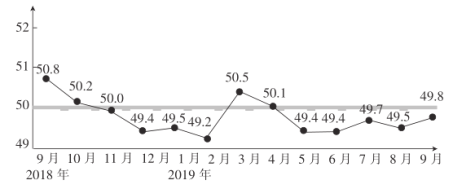
(1)求2019年前9個月我國制造業的采購經理指數的中位數及平均數(精確到0.1);
(2)從2019年4月—2019年9月這6個月任意選取2個月,求這兩個月至少有一個月采購經理指數與上個月相比有所回升的概率.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為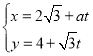 (其中t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,點A的極坐標為
(其中t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,點A的極坐標為![]() ,直線
,直線![]() 經過點A.曲線C的極坐標方程為
經過點A.曲線C的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(2)過點![]() 作直線
作直線![]() 的垂線交曲線C于D,E兩點(D在x軸上方),求
的垂線交曲線C于D,E兩點(D在x軸上方),求![]() 的值.
的值.
查看答案和解析>>
科目: 來源: 題型:
【題目】為了提高生產線的運行效率,工廠對生產線的設備進行了技術改造.為了對比技術改造后的效果,采集了生產線的技術改造前后各20次連續正常運行的時間長度(單位:天)數據,并繪制了如莖葉圖:
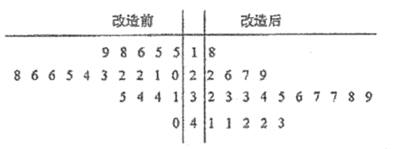
(1)(i)設所采集的40個連續正常運行時間的中位數m,并將連續正常運行時間超過m和不超過m的次數填入下面的列聯表:
超過 | 不超過 | |
改造前 | ||
改造后 |
(ii)根據(i)中的列聯表,能否有99%的把握認為生產線技術改造前后的連續正常運行時間有差異?
附: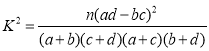
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)工廠的生產線的運行需要進行維護,工廠對生產線的生產維護費用包括正常維護費、保障維護費兩種.對生產線設定維護周期為T天(即從開工運行到第kT天![]() 進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元/次;保障維護費第一次為0.2萬元/周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:
進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元/次;保障維護費第一次為0.2萬元/周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:![]() ,
,![]() .以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列.
.以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列.
查看答案和解析>>
科目: 來源: 題型:
【題目】設各項均為正數的數列![]() 的前n項和為
的前n項和為![]() ,已知
,已知![]() ,且
,且![]() ,對一切
,對一切![]() 都成立.
都成立.
(1)當![]() 時,證明數列
時,證明數列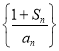 是常數列,并求數列
是常數列,并求數列![]() 的通項公式;
的通項公式;
(2)是否存在實數![]() ,使數列
,使數列![]() 是等差數列?若存在,求出
是等差數列?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖所示的多面體ABCDEF滿足:正方形ABCD與正三角形FBC所在的兩個平面互相垂直,FB∥AE且FB=2EA.
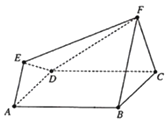
(1)證明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com