【題目】已知函數(shù)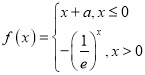
，若存在非零實數(shù)
，使得點
，
都在
的圖象上，則實數(shù)
的取值范圍是______.
【答案】
【解析】
根據(jù)題意，
圖象上至少存在兩點關(guān)于原點對稱，易知
，
的圖象和
，
圖象不關(guān)于原點對稱，則，的圖象與，的圖象存在兩點關(guān)于原點對稱，根據(jù)，的圖象與
，
的圖象關(guān)于原點對稱，轉(zhuǎn)化為，的圖象與，的圖象有交點，即方程
有解，令
，用導(dǎo)數(shù)法求其值域即可.
因為存在非零實數(shù)
，使得點
，
都在的圖象上，
即圖象上至少存在兩點關(guān)于原點對稱，
顯然，的圖象上不存在兩點關(guān)于原點對稱，，的圖象上不存在兩點關(guān)于原點對稱，
因為，的圖象與，的圖象關(guān)于原點對稱，
故問題轉(zhuǎn)化為，的圖象與，的圖象有交點，
即方程
有解，
即有解，
令，當(dāng)時，
，
所以
在
上遞減，
所以
，又當(dāng)
時，
，
所以
，
即實數(shù)
的取值范圍是.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】千百年來，人們一直在通過不同的方式傳遞信息.在古代，烽火狼煙、飛鴿傳書、快馬驛站等通信方式被人們廣泛傳知；第二次工業(yè)革命后，科技的進(jìn)步帶動了電訊事業(yè)的發(fā)展，電報電話的發(fā)明讓通信領(lǐng)域發(fā)生了翻天覆地的變化；之后，計算機和互聯(lián)網(wǎng)的出現(xiàn)則.使得“千里眼”“順風(fēng)耳”變?yōu)楝F(xiàn)實……此時此刻，5G的到來即將給人們的生活帶來顛覆性的變革，“5G領(lǐng)先”一方面是源于我國項層設(shè)計的宏觀布局，另一方面則來自于政府高度重視、企業(yè)積極搶灘、企業(yè)層面的科技創(chuàng)新能力和先發(fā)優(yōu)勢.某科技創(chuàng)新公司基于領(lǐng)先技術(shù)的支持，豐富的移動互聯(lián)網(wǎng)應(yīng)用等明顯優(yōu)勢，隨著技術(shù)的不斷完善，該公司的5G經(jīng)濟(jì)收入在短期內(nèi)逐月攀升，業(yè)內(nèi)預(yù)測，該創(chuàng)新公司在第1個月至第7個月的5G經(jīng)濟(jì)收入y（單位：百萬元）關(guān)于月份x的數(shù)據(jù)如下表：
時間（月份） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
收入（百萬元） | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根據(jù)以上數(shù)據(jù)繪制散點圖：
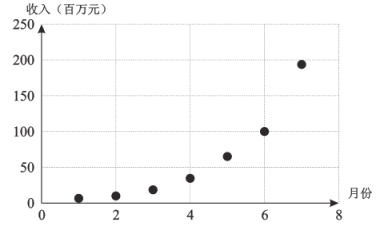
（1）為了更充分運用大數(shù)據(jù)、人工智能、5G等技術(shù)，公司需要派出員工實地考察檢測產(chǎn)品性能和使用狀況，公司領(lǐng)導(dǎo)要從報名的五名科技人員A、B、C、D、E中隨機抽取3個人前往，則A、B同時被抽到的概率為多少？
（2）根據(jù)散點圖判斷，
與
（a，b，c，d均為大于零的常數(shù)）哪一個適宜作為5G經(jīng)濟(jì)收入y關(guān)于月份x的回歸方程類型？（給出判斷即可，不必說明理由）并根據(jù)你判斷結(jié)果及表中的數(shù)據(jù)，求出y關(guān)于x的回歸方程；
（3）請你預(yù)測該公司8月份的5G經(jīng)濟(jì)收入.
參考數(shù)據(jù)：
|
|
|
|
|
|
462 | 10.78 | 2711 | 50.12 | 2.82 | 3.47 |
其中設(shè)
，
參考公式：
對于一組具有線性相關(guān)系的數(shù)據(jù)
（
，2，3，…，n），其回歸直線
的斜率和截距的最小二乘估計公式分別為：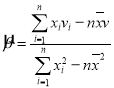
，
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，三棱柱
中，D是
的中點.
（1）證明：
平面
；
（2）若
是邊長為2的正三角形，且
，
，平面
平面
.求平面與側(cè)面所成二面角的正弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在郊野公園的景觀河的兩岸，
、
是夾角為120°的兩條岸邊步道（長度均超過
千米），為方便市民觀光游覽，現(xiàn)準(zhǔn)備在河道拐角處的另一側(cè)建造一個觀景臺
，在兩條步道、上分別設(shè)立游客上下點
、
，從、到觀景臺建造兩條游船觀光線路
、
，測得
千米.
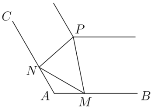
（1）求游客上下點、間的距離；
（2）若
，設(shè)
，求兩條觀光線路與之和關(guān)于
的表達(dá)式
，并求其最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
且在
上的最大值為
，
（1）求函數(shù)f(x)的解析式；
(2)判斷函數(shù)f(x)在（0，π）內(nèi)的零點個數(shù)，并加以證明
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，其中
，
，e為自然對數(shù)的底數(shù).
(1)若
，且當(dāng)
時，
總成立，求實數(shù)a的取值范圍；
(2)若
，且
存在兩個極值點
，
，求證：
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線
（
）上的兩個動點
和
，焦點為F.線段AB的中點為
，且A，B兩點到拋物線的焦點F的距離之和為8.
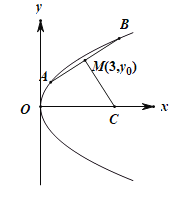
（1）求拋物線的標(biāo)準(zhǔn)方程；
（2）若線段AB的垂直平分線與x軸交于點C，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知a，b，c為正實數(shù)，且滿足a+b+c＝1.證明：
（1）|a
|+|b+c﹣1|
；
（2）（a3+b3+c3）（
）≥3.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
