
【題目】已知![]() ,
,![]() .求證:對任意的
.求證:對任意的![]() 都存在A的一個4元分拆:
都存在A的一個4元分拆: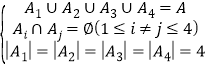 使其中某一個
使其中某一個![]() 的元素恰好是方程
的元素恰好是方程![]() 的一個解.
的一個解.
【答案】見解析
【解析】
依題意,只須證明A中存在4個不同的元素,且某兩個之差等于另兩個之差.
首先,S中兩數之差(大數減小數,以下同)可取1~99共99個值,而A中16個元素可作出![]() 個差.由抽屜原理知,必有2個差是相同的,記為
個差.由抽屜原理知,必有2個差是相同的,記為![]() ,
,
其中![]() ,從而,
,從而,![]() .
.
若![]() ,則命題成立;
,則命題成立;
若![]() ,則取走這一個差
,則取走這一個差![]() (但并不是取走元素
(但并不是取走元素![]() 、
、![]() ),剩下的119個差在1~99之間取值,又必有2個差是相同的,記為
),剩下的119個差在1~99之間取值,又必有2個差是相同的,記為![]() ,其中
,其中![]() ,從而,
,從而,![]() .
.
若![]() ,則命題成立;
,則命題成立;
若![]() ,則取走這一個差
,則取走這一個差![]() ,剩下的118個
,剩下的118個
差在1~99之間取值,又得出必有2個差是相同的.
如此類推,最多進行到第15步時,得出![]() ,其中
,其中![]() ,從而,
,從而,![]() .
.
若![]() ,則命題成立.
,則命題成立.
若![]() ,則前15步積累了15個相同差,
,則前15步積累了15個相同差,
![]() ,①
,①
![]() ,②
,②
……
![]() .
.
由于![]() ,故
,故![]() 不能取A中的最大數也不能取最小數,只有14個可取值,所以,15個
不能取A中的最大數也不能取最小數,只有14個可取值,所以,15個![]() 中必有2個是相同的,不妨設
中必有2個是相同的,不妨設![]() .
.
由于![]() 是在
是在![]() 取走之后才得出的,
取走之后才得出的,
故![]() ,不妨設
,不妨設![]() .
.
①![]() ②得
②得![]() .
.
由![]() ,知
,知![]() ,又
,又![]() ,故
,故![]() ,即
,即![]() 兩兩不等.
兩兩不等.
因此,命題成立.
可見,最多進行到第15步時,必能找出A中4個互不相等的元素a、b、c、d,使得![]() .以這4個元素組成
.以這4個元素組成![]() ,便可滿足題設的全部條件.
,便可滿足題設的全部條件.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的是
①命題“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”;
”;
②若一個命題的逆命題為真命題,則它的否命題也一定為真命題;
③已知![]() 為假命題,則實數
為假命題,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
④我市某校高一有學生![]() 人,高二有學生
人,高二有學生![]() 人,高三有學生
人,高三有學生![]() 人,現采用分層抽樣的方法從該校抽取
人,現采用分層抽樣的方法從該校抽取![]() 個學生作為樣本進行某項調查,則高三被抽取的學生個數為
個學生作為樣本進行某項調查,則高三被抽取的學生個數為![]() 人.
人.
A. ①④ B. ①③④ C. ②④ D. ①②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】齊王有上等,中等,下等馬各一匹;田忌也有上等,中等,下等馬各一匹.田忌的上等馬優于齊王的中等馬,劣于齊王的上等馬;田忌的中等馬優于齊王的下等馬,劣于齊王的中等馬;田忌的下等馬劣于齊王的下等馬.現從雙方的馬匹中隨機各選一匹進行一場比賽,若有優勢的馬一定獲勝,則齊王的馬獲勝的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).在以坐標原點
為參數).在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線
軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() .若直
.若直![]() 與曲線
與曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了堅決打贏新冠狀病毒的攻堅戰,阻擊戰,某小區對小區內的![]() 名居民進行模排,各年齡段男、女生人數如下表.已知在小區的居民中隨機抽取
名居民進行模排,各年齡段男、女生人數如下表.已知在小區的居民中隨機抽取![]() 名,抽到
名,抽到![]() 歲~
歲~![]() 歲女居民的概率是
歲女居民的概率是![]() .現用分層抽樣的方法在全小區抽取
.現用分層抽樣的方法在全小區抽取![]() 名居民,則應在
名居民,則應在![]() 歲以上抽取的女居民人數為( )
歲以上抽取的女居民人數為( )
|
|
| |
女生 |
|
|
|
男生 |
|
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經統計,某校學生上學路程所需要時間全部介于![]() 與
與![]() 之間(單位:分鐘).現從在校學生中隨機抽取
之間(單位:分鐘).現從在校學生中隨機抽取![]() 人,按上學所學時間分組如下:第
人,按上學所學時間分組如下:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得打如圖所示的頻率分布直方圖.
,得打如圖所示的頻率分布直方圖.
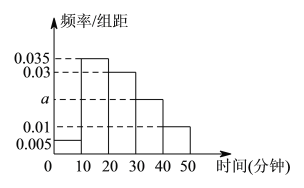
(Ⅰ)根據圖中數據求![]() 的值.
的值.
(Ⅱ)若從第![]() ,
,![]() ,
,![]() 組中用分成抽樣的方法抽取
組中用分成抽樣的方法抽取![]() 人參與交通安全問卷調查,應從這三組中各抽取幾人?
人參與交通安全問卷調查,應從這三組中各抽取幾人?
(Ⅲ)在(Ⅱ)的條件下,若從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加交通安全宣傳活動,求第
人參加交通安全宣傳活動,求第![]() 組至少有
組至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,直線l與橢圓C交于A、B兩點,且
,直線l與橢圓C交于A、B兩點,且![]()
(1)求橢圓C的方程;
(2)若A、B兩點關于原點O的對稱點分別為![]() ,且
,且![]() ,判斷四邊形
,判斷四邊形![]() 是否存在內切的定圓?若存在,請求出該內切圓的方程;若不存在,請說明理由.
是否存在內切的定圓?若存在,請求出該內切圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】郴州市某中學從甲乙兩個教師所教班級的學生中隨機抽取100人,每人分別對兩個教師進行評分,滿分均為100分,整理評分數據,將分數以10為組距分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教師的頻率分布直方圖,和乙教師的頻數分布表:
.得到甲教師的頻率分布直方圖,和乙教師的頻數分布表:

(1)在抽樣的100人中,求對甲教師的評分低于70分的人數;
(2)從對乙教師的評分在![]() 范圍內的人中隨機選出2人,求2人評分均在
范圍內的人中隨機選出2人,求2人評分均在![]() 范圍內的概率;
范圍內的概率;
(3)如果該校以學生對老師評分的中位數是否大于80分作為衡量一個教師是否可評為該年度該校優秀教師的標準,則甲、乙兩個教師中哪一個可評為年度該校優秀教師?(精確到0.1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com