
���}Ŀ���P(gu��n)������![]() ���������Ă�(g��)�Y(ji��)Փ��
���������Ă�(g��)�Y(ji��)Փ��
������C���S��(du��)�Q�D��
������C�P(gu��n)���c(di��n)![]() ����(du��)�Q��
����(du��)�Q��
������C�ϵ��c(di��n)������(bi��o)ԭ�c(di��n)�ľ��x��Сֵ��![]() ��
��
������C�c����(bi��o)�S���ɵĈD�ε���e������![]() ��
��
�����������_�Y(ji��)Փ�ľ�̖(h��o)�ǣ� ��
A.�٢�B.�٢�C.�٢ۢ�D.�ڢۢ�
���𰸡�B
��������
��(du��)�ڢ٣�����C�P(gu��n)��![]() ��(du��)�Q���ʢ����_����(du��)�ڢڣ�
��(du��)�Q���ʢ����_����(du��)�ڢڣ�![]() �P(gu��n)��
�P(gu��n)��![]() ��(du��)�Q�c(di��n)
�Č�(du��)�Q�c(di��n)![]() ��������C�ϣ��ʢ��e(cu��)�`����(du��)�ڢۣ���
��������C�ϣ��ʢ��e(cu��)�`����(du��)�ڢۣ���![]() �ɵ�
�ɵ�![]() ���ɵ�
���ɵ�![]() ���ʢ��e(cu��)�`����(du��)�ڢܣ����Ƶ�����C��ֱ��
���ʢ��e(cu��)�`����(du��)�ڢܣ����Ƶ�����C��ֱ��![]() ���·�����������D�ε���e������
���·�����������D�ε���e������![]() ���ʢ����_��
���ʢ����_��
��(du��)�ڢ٣���?y��n)�����C������һ�c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() ��(du��)�Q�c(di��n)
�Č�(du��)�Q�c(di��n)![]() Ҳ������C�ϣ���������C�P(gu��n)��
Ҳ������C�ϣ���������C�P(gu��n)��![]() ��(du��)�Q���ʢ����_��
��(du��)�Q���ʢ����_��
��(du��)�ڢڣ��@Ȼ�c(di��n)![]() ������C�ϣ���
������C�ϣ���![]() �P(gu��n)��
�P(gu��n)��![]() ��(du��)�Q�c(di��n)��
�Č�(du��)�Q�c(di��n)��![]() ����������C�ϣ��ʢ��e(cu��)�`��
����������C�ϣ��ʢ��e(cu��)�`��
��(du��)�ڢۣ���![]() ƽ���ɵã�
ƽ���ɵã�![]() ����?y��n)?/span>
����?y��n)?/span>![]() ��
��
����![]() ������?y��n)?/span>
������?y��n)?/span>![]() ����(d��ng)�҃H��(d��ng)
����(d��ng)�҃H��(d��ng)![]() �r(sh��)��̖(h��o)�������ʢ��e(cu��)�`��
�r(sh��)��̖(h��o)�������ʢ��e(cu��)�`��
��(du��)�ڢܣ���![]() ֪��
֪��![]() ��
��![]() ����߅ƽ���ɵ�
����߅ƽ���ɵ�![]() ����?y��n)?/span>
����?y��n)?/span>![]() ������
������![]() ��������C��ֱ��
��������C��ֱ��![]() ���·�����������D�ε���e������
���·�����������D�ε���e������![]() ���ʢ����_��
���ʢ����_��
���x��B��


 ��У��������(y��u)���I(y��)���Ӻ���ԇ��ϵ�д�
��У��������(y��u)���I(y��)���Ӻ���ԇ��ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���c(di��n)
���c(di��n)![]() ��E�A
��E�A![]() ��һ�c(di��n).
��һ�c(di��n).
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���^(gu��)�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() ���E�A
���E�A![]() ��
��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����
����![]() ����e.
����e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��ƽ��ֱ������(bi��o)ϵ��(n��i)������![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ��ֱ��
�S�����S��O�S�����O����(bi��o)ϵ��ֱ��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1��������![]() ��ֱ��
��ֱ��![]() ����ֱ������(bi��o)���̣�
����ֱ������(bi��o)���̣�
��2���^(gu��)ԭ�c(di��n)![]() ��һ�l�侀�քe������
��һ�l�侀�քe������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ���c(di��n)���侀������һ�c(di��n)
���c(di��n)���侀������һ�c(di��n)![]() �M��
�M��![]() �����c(di��n)
�����c(di��n)![]() ��܉�E���̣���(xi��)��ֱ������(bi��o)��ʽ����ͨ���̣���
��܉�E���̣���(xi��)��ֱ������(bi��o)��ʽ����ͨ���̣���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() �M��
�M��![]() ����
����![]() .
.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����(d��ng)![]() �r(sh��)������ʽ
�r(sh��)������ʽ![]() �н⣬��(sh��)��(sh��)
�н⣬��(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3���O(sh��)![]() ��
��![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
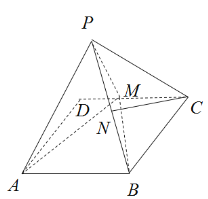
���}Ŀ����D���ھ���![]() �У�
��![]() ��
��![]() ��M��
��M��![]() �ϵ�һ�c(di��n)����
�ϵ�һ�c(di��n)����![]() ���ۺ۰�
���ۺ۰�![]() ����ʹ�c(di��n)D���_(d��)�c(di��n)P��λ�ã���ƽ��
����ʹ�c(di��n)D���_(d��)�c(di��n)P��λ�ã���ƽ��![]() ƽ��
ƽ��![]() .�B��
.�B��![]() ��
��![]() ���c(di��n)N��
���c(di��n)N��![]() �����c(di��n)����
�����c(di��n)����![]() ƽ��
ƽ��![]() .
.
��1����![]() ���L(zh��ng)��
���L(zh��ng)��
��2����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ.
�����J����ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�����_���ǣ� ��
A.�ؚwֱ��һ����(j��ng)�^(gu��)�ӱ��c(di��n)������![]()
B.��ɂ�(g��)���о������P(gu��n)�P(gu��n)ϵ��׃�������P(gu��n)��Խ��(qi��ng)���t�������P(gu��n)ϵ��(sh��)![]() ��ֵԽ�ӽ���1
��ֵԽ�ӽ���1
C.�ښ���D�У������c(di��n)�ֲ���ˮƽ����^(q��)��Խխ���f(shu��)��ģ�͵ĔM�Ͼ���Խ��
D.�ھ��Իؚwģ���У����P(gu��n)ָ��(sh��)![]() Խ�ӽ���1���f(shu��)���ؚwģ�͵ĔM��Ч��Խ��
Խ�ӽ���1���f(shu��)���ؚwģ�͵ĔM��Ч��Խ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1���C������(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ��Ψһ�ĘOֵ�c(di��n)��
��Ψһ�ĘOֵ�c(di��n)��
��2���O(sh��)![]() ��������(sh��)��������ʽ
��������(sh��)��������ʽ![]() ��
��![]() ��(n��i)���������
��(n��i)���������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���b��ÿ�괺����ÿ��15Ԫ�ăr(ji��)��ُ(g��u)��![]() ��̖(h��o)ͯѝ���ɣ����_(k��i)ʼ��ÿ��30Ԫ�ăr(ji��)����ۣ���ǰ2��(g��)��(n��i)��ُ(g��u)�M(j��n)��
��̖(h��o)ͯѝ���ɣ����_(k��i)ʼ��ÿ��30Ԫ�ăr(ji��)����ۣ���ǰ2��(g��)��(n��i)��ُ(g��u)�M(j��n)��![]() ��̖(h��o)ͯѝ�](m��i)�����꣬�t���b�ꌦ(du��)�](m��i)�u����
��̖(h��o)ͯѝ�](m��i)�����꣬�t���b�ꌦ(du��)�](m��i)�u����![]() ��̖(h��o)ͯѝ����ÿ��10Ԫ�ăr(ji��)��̓r(ji��)̎��������(j��)��(j��ng)�(y��n)��1��(g��)��(n��i)��ȫ�܉��
��̖(h��o)ͯѝ����ÿ��10Ԫ�ăr(ji��)��̓r(ji��)̎��������(j��)��(j��ng)�(y��n)��1��(g��)��(n��i)��ȫ�܉��![]() ��̖(h��o)ͯѝ�̓r(ji��)̎���ꮅ����̎���ꮅ��ԓ���Ȳ���ُ(g��u)�M(j��n)
��̖(h��o)ͯѝ�̓r(ji��)̎���ꮅ����̎���ꮅ��ԓ���Ȳ���ُ(g��u)�M(j��n)![]() ��̖(h��o)ͯѝ����ԓ���b��y(t��ng)Ӌ(j��)���^(gu��)ȥ18����ÿ��ԓ����
��̖(h��o)ͯѝ����ԓ���b��y(t��ng)Ӌ(j��)���^(gu��)ȥ18����ÿ��ԓ����![]() ��̖(h��o)ͯѝ��ǰ2��(g��)��(n��i)���N�������Ƴ����±���ע��ҕ�l�ʞ���ʣ���
��̖(h��o)ͯѝ��ǰ2��(g��)��(n��i)���N�������Ƴ����±���ע��ҕ�l�ʞ���ʣ���
ǰ2��(n��i)���N��������λ������ | 30 | 40 | 50 |
�l��(sh��)����λ���꣩ | 6 | 8 | 4 |
��1��������ԓ���ȷ��b��ُ(g��u)�M(j��n)![]() ��̖(h��o)ͯѝ40��������(j��)�y(t��ng)Ӌ(j��)��������ԇ����b��ԓ�����N��
��̖(h��o)ͯѝ40��������(j��)�y(t��ng)Ӌ(j��)��������ԇ����b��ԓ�����N��![]() ��̖(h��o)ͯѝ�@ȡ����(r��n)
��̖(h��o)ͯѝ�@ȡ����(r��n)![]() �ķֲ��к����������Y(ji��)������һλС��(sh��)��
�ķֲ��к����������Y(ji��)������һλС��(sh��)��
��2������(j��)�y(t��ng)Ӌ(j��)������������b��ÿ��ԓ������ُ(g��u)�M(j��n)���ټ�![]() ��̖(h��o)ͯѝ�r(sh��)���@�õ�ƽ������(r��n)���
��̖(h��o)ͯѝ�r(sh��)���@�õ�ƽ������(r��n)���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() �ڈA
�ڈA![]() �ϣ�ֱ��
�ϣ�ֱ��![]() ���E�A��
���E�A��![]() ��
��![]() ���c(di��n)��
���c(di��n)��
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����![]() ��
��![]() ������(bi��o)ԭ�c(di��n)������
������(bi��o)ԭ�c(di��n)������![]() ��ֵ��
��ֵ��
��3���O(sh��)�c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q�c(di��n)��
�S��(du��)�Q�c(di��n)��![]() ��
��![]() �c�c(di��n)
�c�c(di��n)![]() ���غϣ�����ֱ��
���غϣ�����ֱ��![]() �c
�c![]() �S�����c(di��n)
�S�����c(di��n)![]() ��ԇ��(w��n)
��ԇ��(w��n)![]() ����e�Ƿ�������ֵ�������ڣ�����@��(g��)���ֵ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
����e�Ƿ�������ֵ�������ڣ�����@��(g��)���ֵ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com