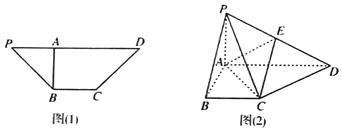
【題目】如圖
在四邊形PBCD中，
，
，
，
，
，沿AB把三角形PAB折起，使P，D兩點的距離為10，得到如圖
所示圖形．
Ⅰ
求證：平面
平面PAC；
Ⅱ若點E是PD的中點，求三棱錐
的體積．
科目：高中數(shù)學 來源： 題型：
【題目】統(tǒng)計表明，某種型號的汽車在勻速行駛中每小時耗油量
（升）關(guān)于行駛速度
（千米/小時）的函數(shù)解析式可以表示為： 
，已知甲、乙兩地相距100千米．
（1）當汽車以40千米/小時的速度勻速行駛時，從甲地到乙地要耗油多少升？
（2）當汽車以多大的速度勻速行駛時，從甲地到乙地耗油最少？最少為多少升？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)
，若數(shù)列
滿足：對所有
，
，且當
時，
，則稱為“
數(shù)列”，設(shè)
R，函數(shù)
，數(shù)列
滿足
，
（
）.
（1）若
，而是
數(shù)列，求
的值；
（2）設(shè)
，證明：存在，使得是
數(shù)列，但對任意，都不是
數(shù)列；
（3）設(shè)
，證明：對任意，都存在，使得是數(shù)列.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面上，給定非零向量
，對任意向量
，定義
.
（1）若
，
，求
；
（2）若
，證明：若位置向量的終點在直線
上，則位置向量的終點也在一條直線上；
（3）已知存在單位向量，當位置向量的終點在拋物線
：
上時，位置向量終點總在拋物線
：
上，曲線和關(guān)于直線
對稱，問直線與向量滿足什么關(guān)系？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，圓C的參數(shù)方程為
為參數(shù)
以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，直線的極坐標方程為
，且圓心C在直線l上．
Ⅰ
求直線l的直角坐標方程及圓C的極坐標方程；
Ⅱ若
是直線l上一點，
是圓C上一點，求
的面積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓方程為
，它的一個頂點為
，離心率
.
（1）求橢圓的方程；
（2）設(shè)直線
與橢圓交于
， 
兩點，坐標原點
到直線
的距離為
，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某電子科技公司由于產(chǎn)品采用最新技術(shù)，銷售額不斷增長，最近
個季度的銷售額數(shù)據(jù)統(tǒng)計如下表（其中
表示
年第一季度，以此類推）：
季度 |
|
|
|
|
|
季度編號x |
|
|
|
|
|
銷售額y（百萬元） |
|
|
|
|
|
（1）公司市場部從中任選
個季度的數(shù)據(jù)進行對比分析，求這個季度的銷售額都超過
千萬元的概率；
（2）求
關(guān)于
的線性回歸方程，并預(yù)測該公司
的銷售額.
附：線性回歸方程：
其中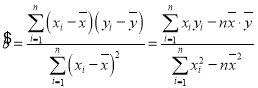
，
參考數(shù)據(jù)：
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，已知圓
經(jīng)過
， 
兩點，且圓心在直線
上．
（1）求圓
的標準方程；
（2）過圓
內(nèi)一點
作兩條相互垂直的弦
，當
時，求四邊形
的面積．
（3）設(shè)直線
與圓
相交于
兩點， 
，且
的面積為
，求直線
的方程．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
