
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,且底面
,且底面![]() 為邊長為2的菱形,
為邊長為2的菱形,![]() ,
,![]() .
.
(Ⅰ)記![]() 在平面
在平面![]() 內的射影為
內的射影為![]() (即
(即![]() 平面
平面![]() ),試用作圖的方法找出M點位置,并寫出
),試用作圖的方法找出M點位置,并寫出![]() 的長(要求寫出作圖過程,并保留作圖痕跡,不需證明過程和計算過程);
的長(要求寫出作圖過程,并保留作圖痕跡,不需證明過程和計算過程);

(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)第(1)問,作圖見解析,再利用射影定理求PM的長. (2) 以D為坐標原點,DA,DE,DP所在直線分別為x軸,y軸,z軸,建立空間直角坐標系D-xyz,利用向量法求二面角![]() 的余弦值.
的余弦值.
試題解析:
(1)取BC中點E,連接DE,PE,在![]() PDE內作DM
PDE內作DM![]() PE,垂足為M,
PE,垂足為M,![]() ,則PM=
,則PM=![]() ,
,
(2)以D為坐標原點,DA,DE,DP所在直線分別為x軸,y軸,z軸,建立空間直角坐標系D-xyz,如圖,A(2,0,0),P(0,0,2),B(1,![]() ,0),C(-1,
,0),C(-1,![]() ,0)
,0)
![]()
分別設平面PAB,平面PBC的法向量為![]() ,則
,則
 ,令
,令![]()
 ,令
,令![]()
![]() , 又二面角A-PB-C的大小為鈍角
, 又二面角A-PB-C的大小為鈍角
二面角A-PB-C的余弦值為![]() .
.


 浙大優(yōu)學小學年級銜接捷徑浙江大學出版社系列答案
浙大優(yōu)學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】某大型超市在2018年元旦舉辦了一次抽獎活動,抽獎箱里放有2個紅球,1個黃球和1個藍球(這些小球除顏色外大小形狀完全相同),從中隨機一次性取2個小球,每位顧客每次抽完獎后將球放回抽獎箱.活動另附說明如下:
①凡購物滿100(含100)元者,憑購物打印憑條可獲得一次抽獎機會;
②凡購物滿188(含188)元者,憑購物打印憑條可獲得兩次抽獎機會;
③若取得的2個小球都是紅球,則該顧客中得一等獎,獎金是一個10元的紅包;
④若取得的2個小球都不是紅球,則該顧客中得二等獎,獎金是一個5元的紅包;
⑤若取得的2個小球只有1個紅球,則該顧客中得三等獎,獎金是一個2元的紅包.
抽獎活動的組織者記錄了該超市前20位顧客的購物消費數(shù)據(jù)(單位:元),繪制得到如圖所示的莖葉圖.

(1)求這20位顧客中獲得抽獎機會的人數(shù)與抽獎總次數(shù)(假定每位獲得抽獎機會的顧客都會去抽獎);
(2)求這20位顧客中獎得抽獎機會的顧客的購物消費數(shù)據(jù)的中位數(shù)與平均數(shù)(結果精確到整數(shù)部分);
(3)分別求在一次抽獎中獲得紅包獎金10元,5元,2元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某河流上的一座水力發(fā)電站,每年六月份的發(fā)電量![]() (單位:萬千瓦時)與該河上游在六月份的降雨量
(單位:萬千瓦時)與該河上游在六月份的降雨量![]() (單位:毫米)有關據(jù)統(tǒng)計,當
(單位:毫米)有關據(jù)統(tǒng)計,當![]() 時,
時, ![]() ;
; ![]() 每增加10,
每增加10, ![]() 增加5.已知近20年
增加5.已知近20年![]() 的值為:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
的值為:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的頻率分布表:近20年六月份降雨量頻率分布表

(2)假定今年六月份的降雨量與近20年六月份降雨量的分布規(guī)律相同,并將頻率視為概率,求今年六月份該水力發(fā)電站的發(fā)電量低于490(萬千瓦時)或超過530(萬千瓦時)的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若數(shù)列![]() 對任意
對任意![]() 滿足
滿足![]() ,下面給出關于數(shù)列
,下面給出關于數(shù)列![]() 的四個命題:①
的四個命題:①![]() 可以是等差數(shù)列,②
可以是等差數(shù)列,②![]() 可以是等比數(shù)列;③
可以是等比數(shù)列;③![]() 可以既是等差又是等比數(shù)列;④
可以既是等差又是等比數(shù)列;④![]() 可以既不是等差又不是等比數(shù)列;則上述命題中,正確的個數(shù)為( )
可以既不是等差又不是等比數(shù)列;則上述命題中,正確的個數(shù)為( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“大眾創(chuàng)業(yè),萬眾創(chuàng)新”是李克強總理在本屆政府工作報告中向全國人民發(fā)出的口號.某生產(chǎn)企業(yè)積極響應號召,大力研發(fā)新產(chǎn)品,為了對新研發(fā)的一批產(chǎn)品進行合理定價,將該產(chǎn)品按事先擬定的價格進行試銷,得到一組銷售數(shù)據(jù)![]()
![]() ,如表所示:
,如表所示:
試銷單價 | 4 | 5 | 6 | 7 | 8 | 9 |
產(chǎn)品銷量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知變量![]() ,
,![]() 具有線性相關關系,求產(chǎn)品銷量
具有線性相關關系,求產(chǎn)品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(Ⅲ)用![]() 表示用(Ⅱ)中所求的線性回歸方程得到的與
表示用(Ⅱ)中所求的線性回歸方程得到的與![]() 對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)
對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)![]() 對應的殘差的絕對值
對應的殘差的絕對值![]() 時,則將銷售數(shù)據(jù)
時,則將銷售數(shù)據(jù)![]() 稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求“好數(shù)據(jù)”至少有一個的概率.
稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求“好數(shù)據(jù)”至少有一個的概率.
(參考公式:線性回歸方程中![]() ,
,![]() 的最小二乘估計分別為
的最小二乘估計分別為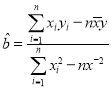 ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中a為實數(shù).
,其中a為實數(shù).
(1)當a=-1時,求函數(shù)y=f(x)的零點;
(2)若f(x)在(-2,2)上為增函數(shù),求實數(shù)a的取值范圍;
(3)對于給定的實數(shù)a,若存在兩個不相等的實數(shù)根![]() ,
,![]() ,(
,(![]() <
<![]() 且
且![]() ≠0)使得f(
≠0)使得f(![]() )=f(
)=f(![]() ),求
),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]()
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)當![]() 時,方程
時,方程![]() 在區(qū)間
在區(qū)間![]() 內有唯一實數(shù)解,求實數(shù)
內有唯一實數(shù)解,求實數(shù)![]() 的取值范圍
的取值范圍
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com