
【題目】某市準備引進優(yōu)秀企業(yè)進行城市建設. 城市的甲地、乙地分別對5個企業(yè)(共10個企業(yè))進行綜合評估,得分情況如莖葉圖所示.

(Ⅰ)根據(jù)莖葉圖,求乙地對企業(yè)評估得分的平均值和方差;
(Ⅱ)規(guī)定得分在85分以上為優(yōu)秀企業(yè). 若從甲、乙兩地準備引進的優(yōu)秀企業(yè)中各隨機選取1個,求這兩個企業(yè)得分的差的絕對值不超過5分的概率.
注:方差![]()
【答案】(Ⅰ)88,48.4.(Ⅱ)![]()
【解析】試題分析:(Ⅰ)直接利用莖葉圖求解乙地對企業(yè)評估得分的平均值和方差即可.
(Ⅱ)甲區(qū)優(yōu)秀企業(yè)得分為88,89,93,95共4個,乙區(qū)優(yōu)秀企業(yè)得分為86,95,96共3個.列出從兩個區(qū)各選一個優(yōu)秀企業(yè),所有基本事件,求出得分的絕對值的差不超過5分的個數(shù).即可求解概率.
試題解析:(Ⅰ)乙地對企業(yè)評估得分的平均值是![]() ,
,
方差是![]() .
.
(Ⅱ)從甲、乙兩地準備引進的優(yōu)秀企業(yè)中各隨機選取1個,有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 組, 設“得分的差的絕對值不超過5分”為事件
組, 設“得分的差的絕對值不超過5分”為事件![]() ,則事件
,則事件![]() 包含有
包含有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 組.
組.
所以![]()
所以得分的差的絕對值不超過5分的概率是![]()


科目:高中數(shù)學 來源: 題型:
【題目】甲罐中有![]() 個紅球,
個紅球,![]() 個白球和
個白球和![]() 個黑球,乙罐中有
個黑球,乙罐中有![]() 個紅球,
個紅球,![]() 個白球和
個白球和![]() 個黑球。先從甲罐中隨機取出一球放入乙罐,分別以
個黑球。先從甲罐中隨機取出一球放入乙罐,分別以![]() 和
和![]() 表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以
表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以![]() 表示由乙罐取出的球是紅球的事件,則下列結論中正確的是________(寫出所有正確結論的編號)。
表示由乙罐取出的球是紅球的事件,則下列結論中正確的是________(寫出所有正確結論的編號)。
①![]() ; ② 事件
; ② 事件![]() 與事件
與事件![]() 相互獨立;③
相互獨立;③![]()
④![]() 是兩兩互斥的事件;
是兩兩互斥的事件;
⑤![]() 的值不能確定,因為它與
的值不能確定,因為它與![]() 中哪一個發(fā)生有關
中哪一個發(fā)生有關
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知四棱錐![]() (圖1)的三視圖如圖2所示,
(圖1)的三視圖如圖2所示,![]() 為正三角形,
為正三角形,![]() 垂直底面
垂直底面![]() ,俯視圖是直角梯形.
,俯視圖是直角梯形.


圖1 圖2
(1)求正視圖的面積;
(2)求四棱錐![]() 的體積;
的體積;
(3)求證:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】△ABC中,a.b.c分別為∠A.∠B.∠C的對邊,如果a.b.c成等差數(shù)列,∠B=30°,△ABC的面積為 ![]() ,那么b等于( )
,那么b等于( )
A.![]()
B.1+ ![]()
C.![]()
D.2+ ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2018年1曰8日,中共中央、國務院隆重舉行國家科學技術獎勵大會,在科技界引發(fā)熱烈反響,自主創(chuàng)新正成為引領經(jīng)濟社會發(fā)展的強勁動力.某科研單位在研發(fā)新產(chǎn)品的過程中發(fā)現(xiàn)了一種新材料,由大數(shù)據(jù)測得該產(chǎn)品的性能指標值![]() 與這種新材料的含量
與這種新材料的含量![]() (單位:克)的關系為:當
(單位:克)的關系為:當![]() 時,
時, ![]() 是
是![]() 的二次函數(shù);當
的二次函數(shù);當![]() 時,
時, ![]() .測得數(shù)據(jù)如表(部分)
.測得數(shù)據(jù)如表(部分)
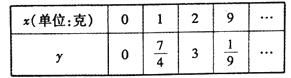
(1)求![]() 關于
關于![]() 的函數(shù)關系式
的函數(shù)關系式![]() ;
;
(2)其函數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知曲線方程![]() ,(
,( ![]() ,
, ![]() ).
).
(![]() )若此方程表示圓,求
)若此方程表示圓,求![]() 的值及
的值及![]() 的范圍.
的范圍.
(![]() )在(
)在(![]() )的條件下,若
)的條件下,若![]() ,直線
,直線![]() 過
過![]() 且與圓相交于
且與圓相交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,求直
,求直
線![]() 方程.
方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系.曲線C的參數(shù)方程為 ![]() (為參數(shù),且0≤<2π),曲線l的極坐標方程為ρ=
(為參數(shù),且0≤<2π),曲線l的極坐標方程為ρ= ![]() (k是常數(shù),且k∈R).
(k是常數(shù),且k∈R).
(1)求曲線C的普通方程和曲線l直角坐標方程;
(2)若曲線l被曲線C截的弦是以( ![]() ,1)為中點,求k的值.
,1)為中點,求k的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com