
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() 的圖像在
的圖像在![]() 處的切線方程為:
處的切線方程為:![]()
(1)求![]() 的值;
的值;
(2)若![]() ,
,![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)a=b=1;(2)(2,+∞).
【解析】
(1)對函數(shù)求導,在切點的導函數(shù)值就是切線的斜率,求出a、b的值;
(2)將原式化簡,變?yōu)樾潞瘮?shù),對新函數(shù)求導討論單調(diào)性求出k的取值;
或是利用參變分離求最值,求得k的取值.
解:(1)f(x) =a![]()
![]() ∴f(1) =a
∴f(1) =a![]() =
=![]() ,f(1)=
,f(1)=![]() =
=![]() ,
,
解得a=b=1
∴f(x)=![]() +
+![]()
(2) (方法1)由![]() +
+![]() <
< ![]() +
+![]() 得,
得,![]() <0,∵x>0∴l(xiāng)nx+(1k)xk+3<0恒成立
<0,∵x>0∴l(xiāng)nx+(1k)xk+3<0恒成立
設(shè)g(x)=lnx+(1k)xk+3 (x>0)
g(x)=![]() +1k=
+1k=![]()
當k≤1時,g(x)≥0,y=g(x)在x(0,+∞)上單調(diào)遞增,不符合題意,舍去
當k>1時,y=g(x)在x(0,![]() )上單調(diào)遞增,在x(
)上單調(diào)遞增,在x(![]() ,+∞)上單調(diào)遞減,
,+∞)上單調(diào)遞減,
∴g(x)≤g(![]() )=ln
)=ln![]() +2k<0
+2k<0
設(shè)h(k)= 2kln(k1),h(k)=1![]() <0,y=h(k)在k(1,+∞)上單調(diào)遞減
<0,y=h(k)在k(1,+∞)上單調(diào)遞減
∵h(2)=0∴由h(k)<0解得k>2
綜上所述,k的取值范圍是(2,+∞).
(方法2)由![]() +
+![]() <
< ![]() +
+![]() 得,
得,![]() <0,∵x>0∴l(xiāng)nx+(1k)xk+3<0恒成立,
<0,∵x>0∴l(xiāng)nx+(1k)xk+3<0恒成立,
整理得:k>![]() ,
,
令g(x)=![]() ,則g(x)=
,則g(x)=![]() .
.
令h(x)= ![]() -lnx-3, (x>0),h(x)= -
-lnx-3, (x>0),h(x)= - ![]() -
- ![]() <0在x>0時恒成立
<0在x>0時恒成立
所以,h(x)單調(diào)遞減,又h(1)=0,
所以,x∈(0,1),h(x)>0,即g(x) >0, g(x)單調(diào)遞增
x∈(1,+∞),h(x)<0, 即g(x) <0, g(x)單調(diào)遞減
g(x)在x=1處有最大值g(1)= 2
所以k>2,k的取值范圍是(2,+∞)


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數(shù)學 來源: 題型:
【題目】由國家公安部提出,國家質(zhì)量監(jiān)督檢驗檢疫總局發(fā)布的《車輛駕駛?cè)藛T血液、呼氣酒精含量閥值與檢驗標準(![]() )》于
)》于![]() 年
年![]() 月
月![]() 日正式實施.車輛駕駛?cè)藛T酒飲后或者醉酒后駕車血液中的酒精含量閥值見表.經(jīng)過反復試驗,一般情況下,某人喝一瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點圖”見圖,
日正式實施.車輛駕駛?cè)藛T酒飲后或者醉酒后駕車血液中的酒精含量閥值見表.經(jīng)過反復試驗,一般情況下,某人喝一瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點圖”見圖,

喝![]() 瓶啤酒的情況
瓶啤酒的情況
且圖表示的函數(shù)模型 ,則該人喝一瓶啤酒后至少經(jīng)過多長時間才可以駕車(時間以整小時計算)?(參考數(shù)據(jù):
,則該人喝一瓶啤酒后至少經(jīng)過多長時間才可以駕車(時間以整小時計算)?(參考數(shù)據(jù):![]() ,
,![]() )
)
( )
駕駛行為類型 | 閥值 |
飲酒后駕車 |
|
醉酒后駕車 |
|
車輛駕車人員血液酒精含量閥值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
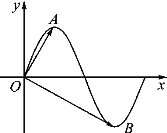
【題目】已知函數(shù)![]() (
(![]() >0)的部分圖象如圖所示,A,B分別是這部分圖象上的最高點、最低點,
>0)的部分圖象如圖所示,A,B分別是這部分圖象上的最高點、最低點,![]() 為坐標原點,若
為坐標原點,若![]() ·
·![]() =0,
=0,![]() 則下列結(jié)論:①函數(shù)
則下列結(jié)論:①函數(shù)![]() 是周期為4的奇函數(shù);②函數(shù)
是周期為4的奇函數(shù);②函數(shù)![]() 是周期為4的偶函數(shù);③函數(shù)
是周期為4的偶函數(shù);③函數(shù)![]() 的最大值是
的最大值是![]() ;④函數(shù)
;④函數(shù)![]() 向左平移
向左平移![]() 個單位后得到的函數(shù)圖象關(guān)于原點對稱;其中錯誤命題的個數(shù)是( )
個單位后得到的函數(shù)圖象關(guān)于原點對稱;其中錯誤命題的個數(shù)是( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知以點A(m, ![]() )(m∈R且m>0)為圓心的圓與x軸相交于O,B兩點,與y軸相交于O,C兩點,其中O為坐標原點.
)(m∈R且m>0)為圓心的圓與x軸相交于O,B兩點,與y軸相交于O,C兩點,其中O為坐標原點.
(1)當m=2時,求圓A的標準方程;
(2)當m變化時,△OBC的面積是否為定值?若是,請求出該定值;若不是,請說明理由;
(3)設(shè)直線![]() 與圓A相交于P,Q兩點,且 |OP|=|OQ|,求 |PQ| 的值.
與圓A相交于P,Q兩點,且 |OP|=|OQ|,求 |PQ| 的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中e為自然對數(shù)的底數(shù).
,其中e為自然對數(shù)的底數(shù).
(1)求證:函數(shù)![]() 是偶函數(shù);
是偶函數(shù);
(2)求證:函數(shù)![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(3)求函數(shù)![]() 在閉區(qū)間
在閉區(qū)間![]() 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() .
. ![]() 表示
表示![]() 中所有不同值的個數(shù).
中所有不同值的個數(shù).
(![]() )設(shè)集合
)設(shè)集合![]() ,
, ![]() ,分別求
,分別求![]() 和
和![]() .
.
(![]() )若集合
)若集合![]() ,求證:
,求證: ![]() .
.
(![]() )
)![]() 是否存在最小值?若存在,求出這個最小值;若不存在,請說明理由.
是否存在最小值?若存在,求出這個最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)有甲、乙兩套設(shè)備生產(chǎn)同一種產(chǎn)品,為了檢測兩套設(shè)備的生產(chǎn)質(zhì)量情況,隨機從兩套設(shè)備生產(chǎn)的大量產(chǎn)品中各抽取了50件產(chǎn)品作為樣本,檢測一項質(zhì)量指標值,若該項質(zhì)量指標值落在![]() 內(nèi),則為合格品,否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表,圖1是乙套設(shè)備的樣本的頻率分布直方圖.
內(nèi),則為合格品,否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表,圖1是乙套設(shè)備的樣本的頻率分布直方圖.
表1:甲套設(shè)備的樣本的頻數(shù)分布表
質(zhì)量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數(shù) | 1 | 4 | 19 | 20 | 5 | 1 |
圖1:乙套設(shè)備的樣本的頻率分布直方圖

(1)填寫下面列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有90%的把握認為該企業(yè)生產(chǎn)的這種產(chǎn)品的質(zhì)量指標值與甲、乙兩套設(shè)備的選擇有關(guān);