
【題目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一點,
上一點,![]() ,且
,且![]() ,則
,則![]() __________.
__________.
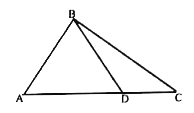
【答案】-4
【解析】分析:先利用同角三角的基本關系求得sinC和sin∠DBC的值,結合∠BDA=C+∠DBC,利用兩角和的余弦公式求得 cos∠BDA 的值,可得∠BDA 的值.
再求出△ABC中各邊的長,再由D是AC上一點,![]() ,我們將相關數據代入平面向量數量積公式即可求解.
,我們將相關數據代入平面向量數量積公式即可求解.
詳解:△ABC中,∵cosC=![]() ,cos∠DBC=
,cos∠DBC=![]() ,
,
∴sinC=![]() ,sin∠DBC=
,sin∠DBC=![]() ,
,
∵∠BDC=π﹣C﹣∠DBC,
∴∠BDA=C+∠DBC,
∴cos∠BDA=cos(C+∠DBC )=cosCcos∠DBC﹣sinCsin∠DBC
=![]() ×
×![]() ﹣
﹣![]() =
=![]() ,
,
∴∠BDA=![]() .
.
設DC=x,BC=a,
在△BDC中,由正弦定理得![]() ,
,
∴a=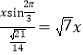 ,
,
在△ABC中,AC=3x,BC=![]() ,AB=2,
,AB=2,
∴cosC=![]() =
=![]() ,解得x=1,∴AD=2,CB=
,解得x=1,∴AD=2,CB=![]() ,
,
∴![]() =2
=2![]() cos(π﹣C)=2
cos(π﹣C)=2![]() (﹣cosC)=﹣2
(﹣cosC)=﹣2![]()
![]() =﹣4.
=﹣4.
故填-4.


科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前n項和為
的前n項和為![]() ,并且滿足
,并且滿足![]() ,
,![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,求
,求![]() ;
;
(3)在(2)的條件下,是否存在常數![]() ,使得數列
,使得數列![]() 為等比數列?若存在,試求出
為等比數列?若存在,試求出![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某飛機失聯,經衛星偵查,其最后出現在小島![]() 附近,現派出四艘搜救船
附近,現派出四艘搜救船![]() ,為方便聯絡,船
,為方便聯絡,船![]() 始終在以小島
始終在以小島![]() 為圓心,100海里為半徑的圓上,船
為圓心,100海里為半徑的圓上,船![]() 構成正方形編隊展開搜索,小島
構成正方形編隊展開搜索,小島![]() 在正方形編隊外(如圖).設小島
在正方形編隊外(如圖).設小島![]() 到
到![]() 的距離為
的距離為![]() ,
,![]() ,
,![]() 船到小島
船到小島![]() 的距離為
的距離為![]() .
.
(1)請分別求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ,并分別寫出定義域;
,并分別寫出定義域;
(2)當![]() 兩艘船之間的距離是多少時搜救范圍最大(即
兩艘船之間的距離是多少時搜救范圍最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的莖葉圖記錄了甲、乙兩組各5名同學的投籃命中次數,乙組記錄中有一個數據模糊,無法確認,在圖中用 ![]() 表示.
表示.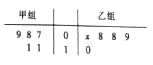
(1)若乙組同學投籃命中次數的平均數比甲組同學的平均數少1,求 ![]() 及乙組同學投籃命中次數的方差;
及乙組同學投籃命中次數的方差;
(2)在(1)的條件下,分別從甲、乙兩組投籃命中次數低于10次的同學中,各隨機選取一名,求這兩名同學的投籃命中次數之和為16的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1: ![]() (t為參數,t ≠ 0),其中0 ≤ α < π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:
(t為參數,t ≠ 0),其中0 ≤ α < π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2: ![]() ,C3:
,C3: ![]() .
.
(1)求C2與C3交點的直角坐標;
(2)若C1與C2相交于點A,C1與C3相交于點B,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是 ![]() 或
或 ![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() ,
, ![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是 ![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的個數為( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分條件;
③命題“若m≤ ![]() ,則方程mx2+2x+2=0有實數根”的否命題為真命題.
,則方程mx2+2x+2=0有實數根”的否命題為真命題.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=Asin(ωx+φ),(0<φ<π)的圖象如圖所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),則sinx0的值為( )
),則sinx0的值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com