【題目】已知恒等式（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n ．
（1）求a1+a2+a3+…+a2n和a2+2a3+22a4+…+22n﹣2a2n的值；
（2）當n≥6時，求證： 
a2+2A 
a3+…+22n﹣2 
a2n＜49n﹣2 ．
【答案】
（1）解：令x=0，則a0=1．
令x=1，則a0+a1+a2+…+a2n=3n，∴a1+a2+…+a2n=3n﹣1．
∵（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n．
∴兩邊對x求導可得：n（1+x+x2）n﹣1=a1+2a2x+…+2na2nx2n﹣1．
令x=0，則n=a1，
由（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n．
令x=2，則 
×7n= 
+ 
+a2+2a3+…+22n﹣2a2n．
∴a2+2a3+…+22n﹣2a2n= 
﹣ ﹣ 
（2）證明：∵（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n．
∴兩邊對x求導可得：n（1+x+x2）n﹣1（1+2x）=a1+2a2x+…+2na2nx2n﹣1，
再一次求導可得：n[（n﹣1）（1+2x）2+2]（1+x+x2）n﹣2=2a2+3×2a3x+…+2n（2n﹣1）a2nx2n﹣2，
=k（k﹣1），
令x=2可得： 
a2+2A 
a3+…+22n﹣2 
a2n=n[25（n﹣1）+2]×7n﹣2，
n≥6時，n[25（n﹣1）+2]＜7n﹣2，
∴ a2+2A a3+…+22n﹣2 a2n=n[25（n﹣1）+2]×7n﹣2＜49n﹣2．
【解析】（1）令x=0，則a0=1．令x=1，a0+a1+a2+…+a2n=3n ， 可得a1+a2+…+a2n ． 由（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n ． 兩邊對x求導可得：n（1+x+x2）n﹣1=a1+2a2x+…+2na2nx2n﹣1 ． 令x=0，可得n=a1 ， 由（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n ． 令x=2，可得 ×7n= + +a2+2a3+…+22n﹣2a2n ． 即可得出．（2）（1+x+x2）n=a0+a1x+a2x2+…+a2nx2n ． 由（1）可得：n（1+x+x2）n﹣1（1+2x）=a1+2a2x+…+2na2nx2n﹣1 ， 兩邊對x求導可得：n[（n﹣1）（1+2x）2+2]（1+x+x2）n﹣2=2a2+3×2a3x+…+2n（2n﹣1）a2nx2n﹣2 ， 令x=2可得： a2+2A a3+…+22n﹣2 a2n=n[25（n﹣1）+2]×7n﹣2 ， n≥6時，n[25（n﹣1）+2]＜7n﹣2 ， 即可證明．
期末復習檢測系列答案
超能學典單元期中期末專題沖刺100分系列答案
黃岡360度定制密卷系列答案
陽光考場單元測試卷系列答案科目：高中數學 來源： 題型：
【題目】設命題p：函數f（x）=lg（ax2﹣x+ 
）的值域為R；命題q：3x﹣9x＜a對一切實數x恒成立，如果命題“p且q”為假命題，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，橢圓C： 
=1（a＞1）的左、右頂點分別為A、B，P是橢圓C上任一點，且點P位于第一象限．直線PA交y軸于點Q，直線PB交y軸于點R．當點Q坐標為（0，1）時，點R坐標為（0，2）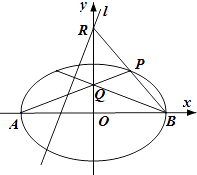 
（1）求橢圓C的標準方程；
（2）求證： 
為定值；
（3）求證：過點R且與直線QB垂直的直線經過定點，并求出該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小學對一年級的甲、乙兩個班進行“數學學前教育”對“小學數學成績優秀”影響的試驗，其中甲班為試驗班(實施了數學學前教育)，乙班為對比班(和甲班一樣進行常規教學，但沒有實施數學學前教育)，在期末測試后得到如下數據：
優秀人數 | 非優秀人數 | 總計 | |
甲班 | 30 | 20 | 50 |
乙班 | 25 | 25 | 50 |
總計 | 55 | 45 | 100 |
能否在犯錯誤的概率不超過0.01的前提下，認為進行“數學學前教育”對“小學數學成績優秀”有積極作用？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓過定點P(4,0),且在y軸上截得的弦MN的長為8.
(1)求動圓圓心C的軌跡方程;
(2)過點(2,0)的直線l與動圓圓心C的軌跡交于A,B兩點,求證:
是一個定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C:
(a>b>0)的離心率為
,以坐標原點O為圓心,橢圓C的短半軸長為半徑的圓與直線x+y+
=0相切.A,B分別是橢圓C的左、右頂點,直線l過B點且與x軸垂直.
(1)求橢圓C的標準方程;
(2)設G是橢圓C上異于A,B的任意一點,過點G作GH⊥x軸于點H,延長HG到點Q使得|HG|=|GQ|,連接AQ并延長交直線l于點M,N為線段MB的中點,判斷直線QN與以AB為直徑的圓O的位置關系,并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知橢圓 
=1（a＞b＞0）的離心率為 
，長軸長為4，過橢圓的左頂點A作直線l，分別交橢圓和圓x2+y2=a2于相異兩點P，Q． 
（1）若直線l的斜率為 
，求 
的值；
（2）若 
=λ 
，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公園準備在一圓形水池里設置兩個觀景噴泉，觀景噴泉的示意圖如圖所示，A，B兩點為噴泉，圓心O為AB的中點，其中OA=OB=a米，半徑OC=10米，市民可位于水池邊緣任意一點C處觀賞． 
（1）若當∠OBC= 
時，sin∠BCO= 
，求此時a的值；
（2）設y=CA2+CB2 ， 且CA2+CB2≤232．
（i）試將y表示為a的函數，并求出a的取值范圍；
（ii）若同時要求市民在水池邊緣任意一點C處觀賞噴泉時，觀賞角度∠ACB的最大值不小于 
，試求A，B兩處噴泉間距離的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
