
��12�֣���֪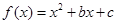 ��ż����(sh��)������
��ż����(sh��)������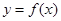 �^�c(di��n)
�^�c(di��n)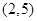 ��
��
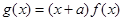 ��
��
��1��������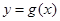 ����б�ʞ�0���о�����(sh��)��(sh��)
����б�ʞ�0���о�����(sh��)��(sh��)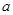 ��ȡֵ������
��ȡֵ������
��2������(d��ng)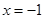 �r����(sh��)
�r����(sh��)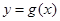 ȡ�ØOֵ���_��
ȡ�ØOֵ���_��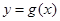 �Ć��{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��: ����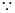
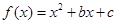 ��ż����(sh��),��
��ż����(sh��),��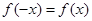 ����
����
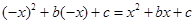 ���
���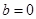
������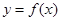 �^�c(di��n)
�^�c(di��n)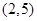 ,��
,��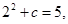 ��
��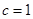
��?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052422432618756395/SYS201205242245085000980482_DA.files/image010.png">�Ķ�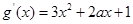 ,
,
����?y��n)�����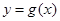 ��б�ʞ�0���о���
��б�ʞ�0���о���
����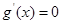 �Ќ�(sh��)��(sh��)��.��
�Ќ�(sh��)��(sh��)��.��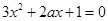 �Ќ�(sh��)��(sh��)��.
�Ќ�(sh��)��(sh��)��.
�˕r��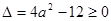 ���
��� 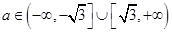
���Ԍ�(sh��)��(sh��)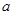 ��ȡֵ����:
��ȡֵ����: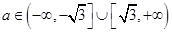
������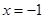 �r����(sh��)
�r����(sh��)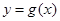 ȡ�ØOֵ,
ȡ�ØOֵ,
����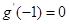 ��
��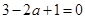 ,���
,���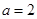
��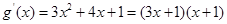
��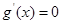 ,��
,��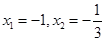
��(d��ng)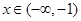 �r,
�r, 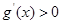 ,��
,��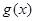 ��
��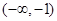 �Ϟ�������(sh��)
�Ϟ�������(sh��)
��(d��ng)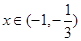 �r,
�r, 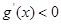 ,��
,��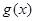 ��
��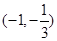 �Ϟ�p����(sh��)
�Ϟ�p����(sh��)
��(d��ng)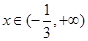 �r,
�r, 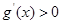 ,��
,��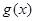 ��
��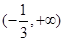 �Ϟ�������(sh��)
�Ϟ�������(sh��)
����������


 �ϴ���o�����������㕽ӽ̳��Ͼ���W(xu��)������ϵ�д�
�ϴ���o�����������㕽ӽ̳��Ͼ���W(xu��)������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��֪![]() ��ż����(sh��)������
��ż����(sh��)������![]() �^�c(di��n)
�^�c(di��n)![]() ��
��![]() ��
��
����������![]() ��б�ʞ�0���о�����(sh��)��(sh��)
��б�ʞ�0���о�����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��������(d��ng)![]() �r����(sh��)
�r����(sh��)![]() ȡ�ØOֵ���_��
ȡ�ØOֵ���_��![]() �Ć��{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2014���|��ʡ�߶��W(xu��)�����п�ԇ?y��n)��Ɣ?sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
��֪ ��ż����(sh��)������
��ż����(sh��)������ �^�c(di��n)��2,5��,
�^�c(di��n)��2,5��, 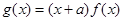 .
.
��1��������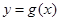 ��б�ʞ�0���о�����(sh��)��(sh��)
��б�ʞ�0���о�����(sh��)��(sh��)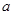 ��ȡֵ������
��ȡֵ������
��2������(d��ng)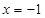 �r����(sh��)
�r����(sh��)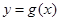 ȡ�ØOֵ���_��
ȡ�ØOֵ���_��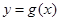 �Ć��{(di��o)�^(q��)�g.
���{(di��o)�^(q��)�g.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011-2012�W(xu��)�긣��ʡ�����������¿��ĿƔ�(sh��)�W(xu��)�������棩 �}�ͣ�����}
��֪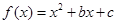 ��ż����(sh��)������
��ż����(sh��)������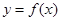 �^�c(di��n)
�^�c(di��n)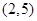 ��
�� 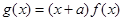 ��
��
������(sh��)��(sh��)b��c��ֵ��
����������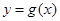 ��б�ʞ�0���о�����(sh��)��(sh��)
��б�ʞ�0���о�����(sh��)��(sh��)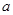 ��ȡֵ������
��ȡֵ������
��������(d��ng)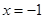 �r����(sh��)
�r����(sh��)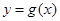 ȡ�ØOֵ���_��
ȡ�ØOֵ���_��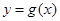 �Ć��{(di��o)�^(q��)�g�͘Oֵ��
�Ć��{(di��o)�^(q��)�g�͘Oֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ���Ĵ�ʡ2010-2011�W(xu��)�����һ�\ģ�M���Ŀƣ� �}�ͣ�����}
(�M��12��)��֪ ��ż����(sh��)������
��ż����(sh��)������ �^�c(di��n)
�^�c(di��n) ����
���� .
.
(��)������ ��б�ʞ�0���о�����(sh��)��(sh��)
��б�ʞ�0���о�����(sh��)��(sh��) ��ȡֵ����
��ȡֵ����
(��)����(d��ng) �r����(sh��)
�r����(sh��)
 ȡ�ØO��ֵ���ҷ���
ȡ�ØO��ֵ���ҷ��� ��������ͬ�Č�(sh��)��(sh��)�⣬��(sh��)��(sh��)
��������ͬ�Č�(sh��)��(sh��)�⣬��(sh��)��(sh��) ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com