【題目】對于給定的正整數(shù)
，如果各項均為正數(shù)的數(shù)列
滿足：對任意正整數(shù)
，
總成立，那么稱
是“
數(shù)列”．
（1）若
是各項均為正數(shù)的等比數(shù)列，判斷
是否為“
數(shù)列”，并說明理由；
（2）若
既是“
數(shù)列”，又是“
數(shù)列”，求證： 
是等比數(shù)列．
【答案】（1）見解析；（2）見解析。
【解析】試題分析：（1）假設(shè){an}是各項均為正數(shù)的等比數(shù)列，由等比數(shù)列的性質(zhì)可得： 
即可證明．
（2）
既是“
數(shù)列”，又是“
數(shù)列”，可得
．可得
對于任意n∈N*（n≥4）都成立．即可證明．
試題解析：（1）
是“
數(shù)列”，理由如下：
因為
是各項均為正數(shù)的等比數(shù)列，不妨設(shè)公比為
．
當(dāng)
時，有
所以
是“
數(shù)列”．
（2）因為
既是“
數(shù)列”，又是“
數(shù)列”，
所以
， 
， ①
， 
． ②
由①得， 
， 
， ③
， 
． ④
③
④
②得， 
， 
．
因為數(shù)列
各項均為正數(shù)，所以
， 
．
所以數(shù)列
從第3項起成等比數(shù)列，不妨設(shè)公比為
．
①中，令
得， 
，所以
．
①中，令
得， 
，所以
．
所以數(shù)列
是公比為
的等比數(shù)列．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四棱錐
中，底面
是梯形， 
， 
， 
， 
，側(cè)面
底面
.
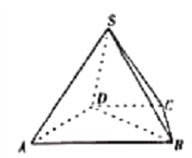
（1）求證：平面
平面
；
（2）若
，且三棱錐
的體積為
，求側(cè)面
的面積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一個幾何體的三視圖如圖所示，其中正視圖與側(cè)視圖是腰長為6的等腰直角三角形，俯視圖是正方形．
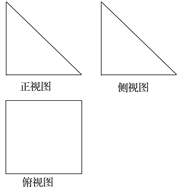
(1)請畫出該幾何體的直觀圖，并求出它的體積；
(2)用多少個這樣的幾何體可以拼成一個棱長為6的正方體ABCD—A1B1C1D1?如何組拼？試證明你的結(jié)論；
(3)在(2)的情形下，設(shè)正方體ABCD—A1B1C1D1的棱CC1的中點為E, 求平面AB1E與平面ABC所成二面角的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖1，在平面多邊形
中，四邊形
為正方形， 
， 
，沿著
將圖形折成圖2，其中
， 
， 
為
的中點．
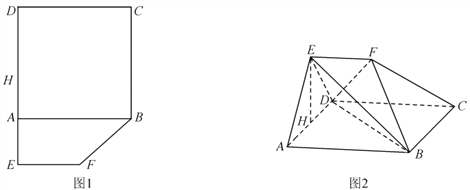
（1）求證： 
；
（2）求四棱錐
的體積．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某企業(yè)有甲、乙兩套設(shè)備生產(chǎn)同一種產(chǎn)品，為了檢測兩套設(shè)備的生產(chǎn)質(zhì)量情況，隨機從兩套設(shè)備生產(chǎn)的大量產(chǎn)品中各抽取了50件產(chǎn)品作為樣本，檢測一項質(zhì)量指標(biāo)值，若該項質(zhì)量指標(biāo)值落在
內(nèi)，則為合格品，否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表，圖1是乙套設(shè)備的樣本的頻率分布直方圖.
表1：甲套設(shè)備的樣本的頻數(shù)分布表
質(zhì)量指標(biāo)值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數(shù) | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設(shè)備的樣本的頻率分布直方圖
（1）填寫下面列聯(lián)表，并根據(jù)列聯(lián)表判斷是否有90%的把握認(rèn)為該企業(yè)生產(chǎn)的這種產(chǎn)品的質(zhì)量指標(biāo)值與甲、乙兩套設(shè)備的選擇有關(guān)；
