【題目】已知函數
，其中
且
．
（1）求函數
的單調區間；
（2）當
時，若存在
，使
成立，求實數
的取值范圍．
【答案】（1）當
時，
的增區間是
，減區間是
，
當
時，的減區間是，增區間是（2）
【解析】
試題分析：（1）先求函數導數
，根據
的正負討論導數符號變化規律，進而得單調區間（2）對應不等式有解問題，一般利用變量分離法，轉化為對應函數最值問題：
最大值，再利用導數求函數
最大值，先求函數導數
，再求導函數零點
，列表分析導函數符號變化規律，進而得出單調性，確定極值與最值
試題解析：（1）定義域為
，．．．．．．．．．．．．．．．．．．．．．．． 2分
當
時，
時，
；
時，
，
當
時，
時，
；時，
．．．．．．．．．．4分
所以當時，的增區間是，減區間是，
當時，的減區間是，增區間是．．．．．．．．．．．．．． 6分
（2）
時，
，由
得：，
設，
，．．．．．．．．．．．．．．．．．．．．．．．8分
所以當
時，
；當
時，
，
所以
在
上遞增，在
上遞減，．．．．．．．．．．．．．．．．．．．．．．．．．．10分
，所以
的取值范圍是．．．．．．．．．．．．．12分
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】國家實行二孩生育政策后，為研究家庭經濟狀況對生二胎的影響，某機構在本地區符合二孩生育政策的家庭中，隨機抽樣進行了調查，得到如下的列聯表：
經濟狀況好 | 經濟狀況一般 | 合計 | |
愿意生二胎 | 50 | ||
不愿意生二胎 | 20 | 110 | |
合計 | 210 |
（1）請完成上面的列聯表，并判斷能否在犯錯誤的概率不超過
的前提下認為家庭經濟狀況與生育二胎有關？
（2）若采用分層抽樣的方法從愿意生二胎的家庭中隨機抽取4個家庭，則經濟狀況好和經濟狀況一般的家庭分別應抽取多少個？
（3）在（2）的條件下，從中隨機抽取2個家庭，求2個家庭都是經濟狀況好的概率．
附：
|
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】集成電路E由3個不同的電子元件組成，現由于元件老化，3個電子元件能正常工作的概率分別降為
，，
，且每個電子元件能否正常工作相互獨立。若3個電子元件中至少有2個正常工作，則E能正常工作，否則就需要維修，且維修集成電路E所需要費用為100元。
(Ⅰ)求集成電路E需要維修的概率；
(Ⅱ)若某電子設備共由2個集成電路E組成，設X為該電子設備需要維修集成電路所需費用。求X的分布列和均值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2016年巴西奧運會的周邊商品有80%左右為“中國制造”,所有的廠家都是經過層層篩選才能獲此殊榮．甲、乙兩廠生產同一產品，為了解甲、乙兩廠的產品質量，以確定這一產品最終的供貨商，采用分層抽樣的方法從甲、乙兩廠生產的產品共98件中分別抽取9件和5件，測量產品中的微量元素的含量（單位：毫克）．下表是從乙廠抽取的5件產品的測量數據：
編號 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
（1）求乙廠生產的產品數量：
（2）當產品中的微量元素
滿足：
，且
時，該產品為優等品．用上述樣本數據估計乙廠生產的優等品的數量：
（3）從乙廠抽出的上述5件產品中，隨機抽取2件，求抽取的2件產品中優等品數的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
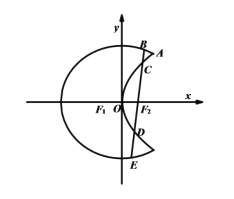
【題目】如圖“月亮圖”是由曲線
與
構成，曲線
是以原點
為中點， 
為焦點的橢圓的一部分，曲線
是以
為頂點， 
為焦點的拋物線的一部分， 
是兩條曲線的一個交點.
（Ⅰ）求曲線
和
的方程；
（Ⅱ）過
作一條與
軸不垂直的直線，分別與曲線
依次交于
四點，若
為
的中點， 
為
的中點，問： 
是否為定值？若是求出該定值；若不是說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】公元263年左右，我國古代數學家劉徽用圓內接正多邊形的面積去逼近圓的面積求圓周率
，劉徽稱這個方法為“割圓術”，并且把“割圓術”的特點概括為“割之彌細，所失彌少，割之又割，以至于不可割，則與圓周合體而無所失矣”，下圖是根據劉徽的“割圓術”思想設計的一個程序框圖，若運行該程序，則輸出的
的值為（ ）（參考數據： 
， 
， 
）
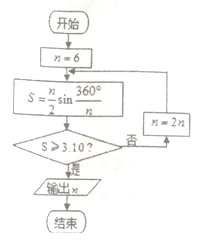
A. 24 B. 30 C. 36 D. 48
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的個數是( )
①命題“x0∈R，x＋1＞3x0”的否定是“x∈R，x2＋1≤3x”；
②“函數f(x)＝cos2ax－sin2ax的最小正周期為π”是“a＝1”的必要不充分條件；
③x2＋2x≥ax在x∈[1,2]上恒成立(x2＋2x)min≥(ax)max在x∈[1,2]上恒成立；
④“平面向量a與b的夾角是鈍角”的充要條件是“a·b＜0”．
A．1 B．2
C．3 D．4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
