
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
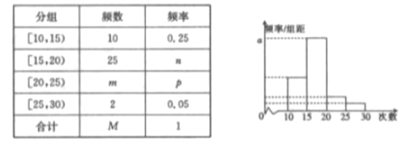
(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)若該校高一學生有800人,試估計該校高一學生參加社區服務的次數在區間![]() 內的人數.
內的人數.
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() 人.
人.
【解析】試題分析:(1)由題意, ![]() 內的頻數是10,頻率是0.25知,
內的頻數是10,頻率是0.25知, ![]() ,所以
,所以![]() ,則
,則![]() ,
, ![]() .(2)高一學生有800人,分組
.(2)高一學生有800人,分組![]() 內的頻率是
內的頻率是![]() ,人數為
,人數為![]() 人.
人.
試題解析:
(1)由![]() 內的頻數是10,頻率是0.25知,
內的頻數是10,頻率是0.25知, ![]() ,所以
,所以![]() .
.
因為頻數之和為40,所以![]() ,
, ![]() .
.
![]() .
.
因為![]() 是對應分組
是對應分組![]() 的頻率與組距的商,所以
的頻率與組距的商,所以![]() .
.
(2)因為該校高一學生有800人,分組![]() 內的頻率是
內的頻率是![]() ,
,
所以估計該校高一學生參加社區服務的次數在此區間內的人數為![]() 人.
人.
【題型】解答題
【結束】
18
【題目】已知直線![]() 經過拋物線
經過拋物線![]() 的焦點
的焦點![]() ,且與
,且與![]() 交于
交于![]() 兩點.
兩點.
(1)設![]() 為
為![]() 上一動點,
上一動點, ![]() 到直線
到直線![]() 的距離為
的距離為![]() ,點
,點![]() ,求
,求![]() 的最小值;
的最小值;
(2)求![]() .
.
科目:高中數學 來源: 題型:
【題目】隨機抽取某高中甲、乙兩個班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖所示.

(1)甲班和乙班同學身高的中位數各是多少?并計算甲班樣本的方差.
(2)現從乙班這10名同學中隨機抽取2名身高不低于173 cm的同學,求身高為176 cm的同學被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 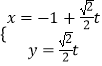 (t為參數),曲線C的極坐標方程是ρ=
(t為參數),曲線C的極坐標方程是ρ= ![]() ,以極點為原點,極軸為x軸正方向建立直角坐標系,點M(﹣1,0),直線l與曲線C交于A、B兩點.
,以極點為原點,極軸為x軸正方向建立直角坐標系,點M(﹣1,0),直線l與曲線C交于A、B兩點.
(Ⅰ)寫出直線l的極坐標方程與曲線C的普通方程;
(Ⅱ)求線段MA、MB長度之積MAMB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數a>0,b>0,函數f(x)=|x﹣a|﹣|x+b|的最大值為3.
(I) 求a+b的值;
(Ⅱ)設函數g(x)=﹣x2﹣ax﹣b,若對于x≥a均有g(x)<f(x),求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos2ωx+ ![]() sin2ωx(ω>0)的最小正周期為π,給出下列四個命題:
sin2ωx(ω>0)的最小正周期為π,給出下列四個命題:
①f(x)的最大值為3;
②將f(x)的圖象向左平移 ![]() 后所得的函數是偶函數;
后所得的函數是偶函數;
③f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增;
]上單調遞增;
④f(x)的圖象關于直線x= ![]() 對稱.
對稱.
其中正確說法的序號是( )
A.②③
B.①④
C.①②④
D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
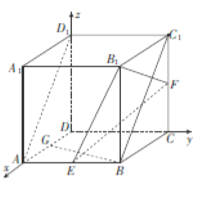
【題目】如圖,在正方體![]() 中,
中, ![]() 分別是棱
分別是棱![]() 的中點,
的中點, ![]() 為棱
為棱![]() 上一點,且異面直線
上一點,且異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
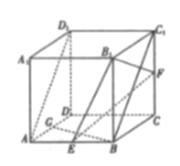
(1)證明: ![]() 為
為![]() 的中點;
的中點;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)以![]() 為坐標原點,建立如圖所示的空間直角坐標系
為坐標原點,建立如圖所示的空間直角坐標系![]() ,不妨令正方體的棱長為2,設
,不妨令正方體的棱長為2,設![]() ,利用
,利用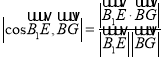 ,解得
,解得![]() ,即可證得;
,即可證得;
(2)分別求得平面![]() 與平面
與平面![]() 的法向量
的法向量![]() ,利用
,利用![]() 求解即可.
求解即可.
試題解析:
(1)證明:以![]() 為坐標原點,建立如圖所示的空間直角坐標系
為坐標原點,建立如圖所示的空間直角坐標系![]() .
.
不妨令正方體的棱長為2,
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
設![]() ,則
,則![]() ,
, ![]() ,
,
所以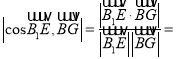
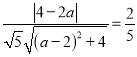 ,
,
所以![]() ,解得
,解得![]() (
(![]() 舍去),即
舍去),即![]() 為
為![]() 的中點.
的中點.
(2)解:由(1)可得![]() ,
, ![]() ,
,
設![]() 是平面
是平面![]() 的法向量,
的法向量,
則![]() .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以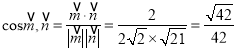 .
.
所以所求銳二面角的余弦值為![]() .
.
點睛:空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.
【題型】解答題
【結束】
22
【題目】已知橢圓![]() 的短軸長為2,且橢圓
的短軸長為2,且橢圓![]() 過點
過點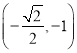 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 過定點
過定點![]() ,且斜率為
,且斜率為![]() ,若橢圓
,若橢圓![]() 上存在
上存在![]() 兩點關于直線
兩點關于直線![]() 對稱,
對稱, ![]() 為坐標原點,求
為坐標原點,求![]() 的取值范圍及
的取值范圍及![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,焦點在坐標軸上,焦距長為2,左準線為
的中心在坐標原點,焦點在坐標軸上,焦距長為2,左準線為![]() :
: ![]() .
.
(1)求橢圓![]() 的方程及其離心率;
的方程及其離心率;
(2)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() 為線段
為線段![]() 的中點,求直線
的中點,求直線![]() 的方程;
的方程;
(3)過橢圓![]() 右準線
右準線![]() 上任一點
上任一點![]() 引圓
引圓![]() :
: ![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,
, ![]() .試探究直線
.試探究直線![]() 是否過定點?若過定點,請求出該定點;否則,請說明理由.
是否過定點?若過定點,請求出該定點;否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓錐OO1的體積為![]() π.設它的底面半徑為x,側面積為S.
π.設它的底面半徑為x,側面積為S.
(1)試寫出S關于x的函數關系式;
(2)當圓錐底面半徑x為多少時,圓錐的側面積最小?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() :
:![]() ,拋物線
,拋物線![]() 的準線與
的準線與![]() 交于點
交于點![]() .
.
(1)過![]() 作曲線
作曲線![]() 的切線,設切點為
的切線,設切點為![]() ,
, ![]() ,證明:以
,證明:以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ;
;
(2)過點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() 、
、![]() ,
, ![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,
兩點, ![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() ,
, ![]() 的中點分別為
的中點分別為![]() 、
、![]() ,試討論直線
,試討論直線![]() 是否過定點?若過,求出定點的坐標;若不過,請說明理由.
是否過定點?若過,求出定點的坐標;若不過,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com