【題目】如果函數f（x）=（x﹣1）2+1定義在區間[t，t+1]上，求f（x）的最小值．
【答案】解：函數f（x）=（x﹣1）2+1對稱軸方程為x=1，
頂點坐標為（1，1），圖象開口向上，
若頂點橫坐標在區間[t，t+1]左側時，
有1＜t，此時，當x=t時，函數取得最小值 
．
若頂點橫坐標在區間[t，t+1]上時，
有t≤1≤t+1，即0≤t≤1．當x=1時，函數取得最小值f（x）min=f（1）=1．
若頂點橫坐標在區間[t，t+1]右側時，
有t+1＜1，即t＜0．當x=t+1時，函數取得最小值 
綜上討論，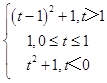 
【解析】根據二次函數的大小求出函數的對稱軸，通過討論t的范圍，求出函數的最小值即可．
【考點精析】認真審題，首先需要了解函數的最大(小)值與導數(求函數
在
上的最大值與最小值的步驟：（1）求函數在
內的極值；（2）將函數的各極值與端點處的函數值
，
比較，其中最大的是一個最大值，最小的是最小值)．
科目：高中數學 來源： 題型：
【題目】已知集合A={x||x+1|＜1}，B={x|y= 
，y∈R}，則A∩RB=（ ）
A.（﹣2，1）
B.（﹣2，﹣1]
C.（﹣1，0）
D.[﹣1，0）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）滿足f（0）=2和f（x+1）﹣f（x）=2x﹣1對任意實數x都成立．
（1）求函數f（x）的解析式；
（2）當t∈[﹣1，3]時，求y=f（2t）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=kx，g（x）= 
．
（1）求函數g（x）= 的單調區間；
（2）若不等式f（x）≥g（x）在區間（0，+∞）上恒成立，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=cos（2x﹣ 
）+2sin（x﹣ 
）cos（x﹣ ）．
（1）求函數f（x）的最小正周期和圖象的對稱軸方程．
（2）求函數f（x）在區間[﹣ 
， 
]上的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，拋物線
的焦點均在
軸上， 
的中心和
的頂點均為原點
，從每條曲線上各取兩個點，其坐標分別是
， 
， 
， 
．
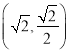（1）求
， 
的標準方程；
（2）是否存在直線
滿足條件：①過
的焦點
；②與
交于不同的兩點
且滿足
？若存在，求出直線方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知冪函數f（x）滿足：對任意x1 ， x2∈R，當且僅當x1=x2時，有f（x1）=f（x2）．則f（﹣1）+f（0）+f（1）的值為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
