
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,過
,過![]() 且與
且與![]() 軸垂直的直線與橢圓
軸垂直的直線與橢圓![]() 在第一象限內(nèi)的交點為
在第一象限內(nèi)的交點為![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,當
兩點,當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】試題分析:(1)由題意得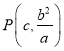 ,
, ![]() ,∴
,∴![]() .①∵
.①∵![]() ,∴
,∴![]() .②聯(lián)立①②得a,b,c即得橢圓
.②聯(lián)立①②得a,b,c即得橢圓![]() 的方程(2)設(shè)直線
的方程(2)設(shè)直線![]() 方程為:
方程為: ![]() ,
, ![]() 點坐標為
點坐標為![]() ,
, ![]() 點坐標為
點坐標為![]() .聯(lián)立
.聯(lián)立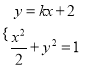 得
得![]() ,根據(jù)韋達定理由弦長公式得,
,根據(jù)韋達定理由弦長公式得, 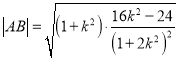 ,又點
,又點![]() 到直線
到直線![]() 的距離
的距離![]() ,
, 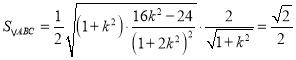 ,解得k值,即得直線
,解得k值,即得直線![]() 的方程.
的方程.
試題解析:
(1)設(shè)![]() ,
, ![]() ,則
,則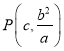 ,
,
∵![]() ,∴
,∴![]() .①
.①
∵![]() ,∴
,∴![]() .②
.②
聯(lián)立①②得, ![]() ,
, ![]() ,
, ![]() .
.
∴橢圓方程為![]() .
.
(2)顯然直線![]() 斜率存在,設(shè)直線
斜率存在,設(shè)直線![]() 方程為:
方程為: ![]() ,
, ![]() 點坐標為
點坐標為![]() ,
, ![]() 點坐標為
點坐標為![]() .
.
聯(lián)立方程組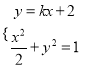 ,得
,得![]() ,
,
令![]() 得,
得, ![]() ,
,
∴![]() ,
, ![]() ,
,
由弦長公式得, ![]()
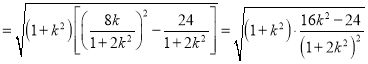 ,
,
點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
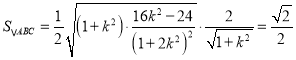 ,解得
,解得![]() .
.
∴![]() 的方程為:
的方程為: ![]() .
.


科目:高中數(shù)學 來源: 題型:
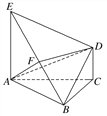
【題目】如圖所示,底面ABC為正三角形,EA⊥平面ABC,DC⊥平面ABC,EA=AB=2DC=2a,設(shè)F為EB的中點.
(1)求證:DF∥平面ABC;
(2)求直線AD與平面AEB所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,△ABC內(nèi)接于圓柱的底面圓O,AB是圓O的直徑,AB=2,BC=1,DC、EB是兩條母線,且tan∠EAB=![]() .
.
(1)求三棱錐C-ABE的體積;
(2)證明:平面ACD⊥平面ADE;
(3)在CD上是否存在一點M,使得MO∥平面ADE,證明你的結(jié)論.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】心理學家發(fā)現(xiàn)視覺和空間能力與性別有關(guān),某數(shù)學興趣小組為了驗證這個結(jié)論,從興趣小組中按分層抽樣的方法抽取50名同學,給所有同學幾何和代數(shù)各一題,讓各位同學自由選擇一道題進行解答.統(tǒng)計情況如下表:(單位:人)
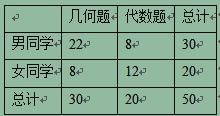
(1)能否據(jù)此判斷有![]() 的把握認為視覺和空間能力與性別有關(guān)?
的把握認為視覺和空間能力與性別有關(guān)?
(2)經(jīng)過多次測試發(fā)現(xiàn):女生甲解答一道幾何題所用的時間在5—7分鐘,女生乙解答一道幾何題所用的時間在6—8分鐘,現(xiàn)甲、乙兩人獨立解答同一道幾何題,求乙比甲先解答完的概率;
(3)現(xiàn)從選擇幾何題的8名女生中任意抽取兩人對她們的答題情況進行研究,記甲、乙兩名女生被抽到的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
附表及公式

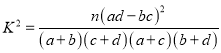
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求
,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若關(guān)于![]() 的不等式
的不等式![]() 對一切
對一切![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓C: ![]() 的左、右頂點分別為A1、A2,點P在C上且直線PA2的斜率的取值范圍是[-2,-1],那么直線PA1斜率的取值范圍是________.
的左、右頂點分別為A1、A2,點P在C上且直線PA2的斜率的取值范圍是[-2,-1],那么直線PA1斜率的取值范圍是________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com