
解答題
對于在區間[m,n]上有意義的兩個函數f(x)與g(x),如果對任意的x∈[m,n],均有|f(x)-g(x)|≤1,則稱f(x)與g(x)在[m,n]上是接近的,否則稱f(x)與g(x)在[m,n]上是非接近的.現有兩個函數f1(x)=loga(x-3a)與f2(x)=loga![]() (a>0且a≠1),給定區間[a+2,a+3].
(a>0且a≠1),給定區間[a+2,a+3].
(1)若f1(x)與f2(x)在給定區間[a+2,a+3]上都有意義,求a的取值范圍;
(2)討論f1(x)與f2(x)在給定區間[a+2,a+3]上是否是接近的.
|
解:(1)依題意a>0且a≠1. 又 ∴0<a<1. (2)|f1(x)-f2(x)|=|loga(x2-4ax+3a2)|. 令|f1(x)-f2(x)|≤1,得 -1≤loga(x2-4ax+3a2)≤1. (*) ∵0<a<1, ∴[a+2,a+3]在x=2a的右側. ∴g(x)=loga(x2-4ax+3a2)在[a+2,a+3]上為減函數, 從而g(x)max=g(a+2)=loga(4-4a),g(x)min=g(a+3)=loga(9-6a). 于是(*)成立的充要條件是 解得0<a≤ 故當0<a≤ 當 |


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源:2004全國各省市高考模擬試題匯編(天利38套)·數學 題型:044
對于函數y=f(x)(x∈D,D是此函數的定義域)若同時滿足下列條件:
(Ⅰ)f(x)在D內單調遞增或單調遞減;
(Ⅱ)存在區間[a,b]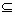 D,使f(x)在[a,b]上的值域為[a,b];那么,把y=f(x)(x∈D)叫閉函數.
D,使f(x)在[a,b]上的值域為[a,b];那么,把y=f(x)(x∈D)叫閉函數.
(1)求閉函數y=-x3符合條件(Ⅱ)的區間[a,b];
(2)判斷函數f(x)=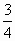 x+
x+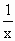 (x∈R+)是否為閉函數?并說明理由;
(x∈R+)是否為閉函數?并說明理由;
(3)若y=k+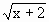 是閉函數,求實數k的取值范圍.
是閉函數,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源:東北師大附中2006—2007學年度上學期高三年級第二次質量檢測、數學(文)試題 題型:044
| |||||||||||||||
查看答案和解析>>
科目:高中數學 來源:東北師大附中2006—2007學年度上學期高三年級第二次質量檢測、數學(理)試題 題型:044
| |||||||||||||||
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com