
已知二次函數f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上為單調遞增函數,求實數a的取值范圍;
(ii)若b=﹣1,c=1,當x∈[0,1]時,|f(x)|的最大值為1,求實數a的取值范圍;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有兩個小于1的不等正根,求a的最小正整數值.
(Ⅰ)(i)[1,+∞);(ii)(0,1];(Ⅱ)5
解析試題分析:(Ⅰ)(i)若b=﹣2,則f(x)=ax2﹣2x+c(a>0)的圖象是開口朝上且以直線x= 為對稱軸的拋物線.若f(x)在(1,+∞)上為單調遞增函數,則
為對稱軸的拋物線.若f(x)在(1,+∞)上為單調遞增函數,則 ≤1,解得a≥1,即實數a的取值范圍為[1,+∞);(ii)若b=﹣1,c=1,則f(x)=ax2﹣x+1(a>0)的圖象是開口朝上且以直線x=
≤1,解得a≥1,即實數a的取值范圍為[1,+∞);(ii)若b=﹣1,c=1,則f(x)=ax2﹣x+1(a>0)的圖象是開口朝上且以直線x= 為對稱軸的拋物線,若當x∈[0,1]時,|f(x)|的最大值為1,則
為對稱軸的拋物線,若當x∈[0,1]時,|f(x)|的最大值為1,則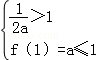 或
或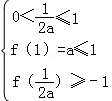 解得0<a<
解得0<a<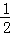 ,或
,或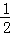 ≤a≤1,所以實數a的取值范圍為(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有兩個小于1的不等正根,則
≤a≤1,所以實數a的取值范圍為(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有兩個小于1的不等正根,則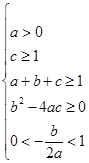
解得a>4,故a的最小正整數值為5.
試題解析:(Ⅰ)(i)若b=﹣2,
則f(x)=ax2﹣2x+c(a>0)的圖象是開口朝上且以直線x= 為對稱軸的拋物線.
為對稱軸的拋物線.
若f(x)在(1,+∞)上為單調遞增函數,則 ≤1,解得a≥1,
≤1,解得a≥1,
即實數a的取值范圍為[1,+∞)
(ii)若b=﹣1,c=1,
則f(x)=ax2﹣x+1(a>0)的圖象是開口朝上且以直線x= 為對稱軸的拋物線.
為對稱軸的拋物線.
若當x∈[0,1]時,|f(x)|的最大值為1,
則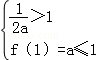 或
或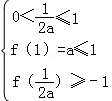 ,
,
解得0<a<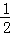 ,或
,或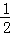 ≤a≤1
≤a≤1
綜上所述:0<a≤1
即實數a的取值范圍為(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有兩個小于1的不等正根,
則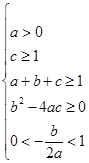
由b2>4ac>4a(1﹣a﹣b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2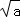 ,
,
即b>2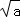 ﹣2a,…①
﹣2a,…①
由b2>4ac≥4a得:
b<﹣2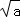 …②
…②
由①②得:
2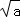 ﹣2a<﹣2
﹣2a<﹣2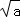 ,
,
解得a>4,
故a的最小正整數值為5.
考點:1.二次函數的圖象與性質;2.不等式的性質


科目:高中數學 來源: 題型:解答題
某市糧食儲備庫的設計容量為30萬噸,年初庫存糧食10萬噸,從1月份起,計劃每月收購糧食M萬噸,每月供給市面粉廠糧食1萬噸,另外每月還有大量的糧食外調任務。已知n個月內外調糧食的總量為 萬噸與n的函數關系為
萬噸與n的函數關系為 .要使在16個月內每月糧食收購之后能滿足內、外調需要,且每月糧食調出后糧庫內有不超過設計容量的儲備糧,求M的范圍。
.要使在16個月內每月糧食收購之后能滿足內、外調需要,且每月糧食調出后糧庫內有不超過設計容量的儲備糧,求M的范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在自然條件下,某草原上野兔第n年年初的數量記為xn,該年的增長量yn和 xn與 的乘積成正比,比例系數為
的乘積成正比,比例系數為 ,其中m是與n無關的常數,且x1<m,
,其中m是與n無關的常數,且x1<m,
(1)證明: ;
;
(2)用 xn表示xn+1;并證明草原上的野兔總數量恒小于m.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
記不超過x的最大整數為 ,令
,令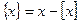 ,則函數
,則函數 : ①定義域為R; ②值域為
: ①定義域為R; ②值域為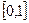 ;③在定義域上是單調增函數; ④是周
;③在定義域上是單調增函數; ④是周 期為1的周期函數; ⑤是奇函數。其中正確判斷的序號是_________________(把所有正確的序號都填上)
期為1的周期函數; ⑤是奇函數。其中正確判斷的序號是_________________(把所有正確的序號都填上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com