
【題目】如圖,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.
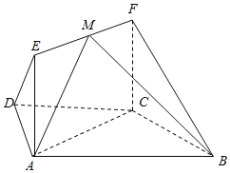
(1)求證:![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的平面角為
所成銳二面角的平面角為![]() ,且滿足
,且滿足![]() ?若不存在,請說明理由;若存在,求出
?若不存在,請說明理由;若存在,求出![]() 的長度.
的長度.
【答案】(1)見解析(2)在線段![]() 上存在點
上存在點![]() 滿足題意,
滿足題意,![]() .
.
【解析】
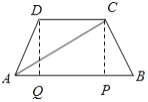
(1)如圖所示的等腰梯形![]() 中,經過點
中,經過點![]() ,
,![]() 分別作
分別作![]() ,
,![]() ,垂足為
,垂足為![]() .利用矩形的性質可求出
.利用矩形的性質可求出![]() ,在
,在![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() ,利用勾股定理的逆定理可得
,利用勾股定理的逆定理可得![]() ,再利用面面垂直的性質定理即可證明
,再利用面面垂直的性質定理即可證明![]() 平面
平面![]() ;
;
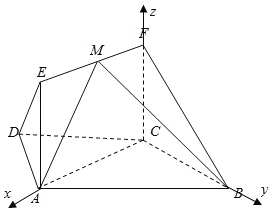
(2)如圖所示,建立空間直角坐標系.設![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,可得
,可得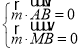 ,取平面
,取平面![]() 的法向量
的法向量![]() ,利用
,利用![]() ,
,![]() ,即可求出.
,即可求出.
(1)如圖所示的等腰梯形![]() 中,經過點
中,經過點![]() ,
,![]() 分別作
分別作![]() ,
,![]() ,垂足為
,垂足為![]() ,則
,則![]() 為矩形,
為矩形,![]() .在
.在![]() 中,
中,![]() ,則
,則![]() ,
,
同理可得![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又∵四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)如圖所示,建立空間直角坐標系.
![]() ,
,![]() ,
,![]() ,設
,設![]() ,
,
![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則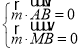 ,∴
,∴ 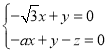
取![]() .
.
取平面![]() 的法向量
的法向量![]() .
.
由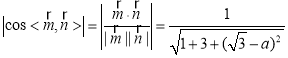 ,
,
由題意可得: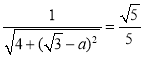 ,
,![]() .
.
解得![]() .
.
因此在線段![]() 上點
上點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的平面角為
所成銳二面角的平面角為![]() ,且滿足
,且滿足![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】一項針對都市熟男(三線以上城市,![]() 歲男性)消費水平的調查顯示,對于最近一年內是否購買過以下七類高價商品,全體被調查者,以及其中包括的1980年及以后出生(80后)被調查者,1980年以前出生(80前)被調查者回答“是”的比例分別如下:
歲男性)消費水平的調查顯示,對于最近一年內是否購買過以下七類高價商品,全體被調查者,以及其中包括的1980年及以后出生(80后)被調查者,1980年以前出生(80前)被調查者回答“是”的比例分別如下:
全體被調查者 | 80后被調查者 | 80前被調查者 | |
電子產品 | 56.9% | 66.0% | 48.5% |
服裝 | 23.0% | 24.9% | 21.2% |
手表 | 14.3% | 19.4% | 9.7% |
運動、戶外用品 | 10.4% | 11.1% | 9.7% |
珠寶首飾 | 8.6% | 10.8% | 6.5% |
箱包 | 8.1% | 11.3% | 5.1% |
個護與化妝品 | 6.6% | 6.0% | 7.2% |
以上皆無 | 25.3% | 17.9% | 32.1% |
根據表格中數據判斷,以下分析錯誤的是( )
A. 都市熟男購買比例最高的高價商品是電子產品
B. 從整體上看,80后購買高價商品的意愿高于80前
C. 80前超過3成一年內從未購買過表格中七類高價商品
D. 被調查的都市熟男中80后人數與80前人數的比例大約為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為參數,且
為參數,且![]() .
.
(Ⅰ)當![]() 時,判斷函數
時,判斷函數![]() 是否有極值;
是否有極值;
(Ⅱ)要使函數![]() 的極小值大于零,求參數
的極小值大于零,求參數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若對(Ⅱ)中所求的取值范圍內的任意函數![]() ,函數
,函數![]() 在區間
在區間![]() 內都是增函數,求實數
內都是增函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產該零件的流水線上隨機抽取100個零件為樣本,測量其直徑后,整理得到下表:
生產該零件的流水線上隨機抽取100個零件為樣本,測量其直徑后,整理得到下表:
直徑/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直徑/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(I)為評判一臺設備的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,并根據以下不等式進行判定(
,并根據以下不等式進行判定(![]() 表示相應事件的概率):①
表示相應事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定規則為:若同時滿足上述三個式子,則設備等級為甲;若僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部都不滿足,則等級為丁.試判斷設備
.判定規則為:若同時滿足上述三個式子,則設備等級為甲;若僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部都不滿足,則等級為丁.試判斷設備![]() 的性能等級.
的性能等級.
(Ⅱ)將直徑尺寸在![]() 之外的零件認定為是“次品”,將直徑尺寸在
之外的零件認定為是“次品”,將直徑尺寸在![]() 之外的零件認定為“突變品”.從樣本的“次品”中隨意抽取兩件,求至少有一件“突變品”的概率.
之外的零件認定為“突變品”.從樣本的“次品”中隨意抽取兩件,求至少有一件“突變品”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() ,四點
,四點![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三點在橢圓
中恰有三點在橢圓![]() 上.
上.
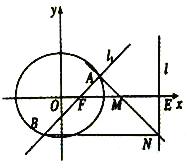
(I)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過![]() 的右焦點
的右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() 為線段
為線段![]() 的中點,過點
的中點,過點![]() 作直線
作直線![]() 于點
于點![]() .證明:
.證明:![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國古代數學家、天文學家大約在公元222年趙爽為《周碑算經》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”(以弦為邊長得到的正方形是由4個全等的直角三角形再加上中間的一個小正方形組成的)類比“趙爽弦圖”,趙爽弦圖可類似地構造如圖所示的圖形,它是由個3全等的等邊三角形與中間的一個小等邊三角形組成的一個大等邊三角形,設DF2AF,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點為原點,其焦點
的頂點為原點,其焦點![]() 到直線
到直線![]() 的距離為
的距離為![]() .設
.設![]() 為直線
為直線![]() 上的點,過點
上的點,過點![]() 作拋物線
作拋物線![]() 的兩條切線
的兩條切線![]() ,其中
,其中![]() 為切點.
為切點.
(1) 求拋物線![]() 的方程;
的方程;
(2) 當點![]() 為直線
為直線![]() 上的定點時,求直線
上的定點時,求直線![]() 的方程;
的方程;
(3) 當點![]() 在直線
在直線![]() 上移動時,求
上移動時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x2+1)﹣e﹣|x|(e為自然對數的底數),則不等式f(2x+1)>f(x)的解集是( )
A. (﹣1,1)B. (﹣∞,﹣1)∪(1,+∞)
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com