
【題目】在幾何體![]() 中,如圖,四邊形
中,如圖,四邊形![]() 為平行四邊形,
為平行四邊形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
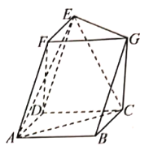
(1)求證:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(1)由![]() ,得到平面
,得到平面![]() ,平面
,平面![]() ,根據平面
,根據平面![]() 平面
平面![]() ,由面面平行的性質定理得到
,由面面平行的性質定理得到![]() ,進而得到四邊形
,進而得到四邊形![]() 為平行四邊形,再根據
為平行四邊形,再根據![]() 平面
平面![]() ,得到
,得到![]() ,由
,由![]() ,得到
,得到![]() ,同理得到
,同理得到![]() ,由線面垂直的判定定理得到
,由線面垂直的判定定理得到![]() 平面
平面![]() 得證.
得證.
(2)由(1)可知,直線![]() 、
、![]() 、
、![]() 兩兩垂直.以
兩兩垂直.以![]() 為坐標原點,以
為坐標原點,以![]() 、
、![]() 、
、![]() 為坐標軸建立的空間直角坐標系
為坐標軸建立的空間直角坐標系![]() ,設
,設![]() ,則
,則![]() ,
,![]() ,分別求得平面
,分別求得平面![]() 和平面
和平面![]() 的一個法向量
的一個法向量![]() ,代入
,代入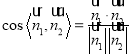 求解.
求解.
(1)證明:由![]() ,
,
可知![]() 、
、![]() 、
、![]() 、
、![]() 四點確定平面
四點確定平面![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 四點確定平面
四點確定平面![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,四邊形
,四邊形![]() 為平行四邊形.
為平行四邊形.
同理可得,四邊形![]() 為平行四邊形,四邊形
為平行四邊形,四邊形![]() 為平行四邊形.
為平行四邊形.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
而![]() ,于是
,于是![]() .
.
由![]() ,
,![]() ,
,
則![]() .
.
由![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由(1)可知,直線![]() 、
、![]() 、
、![]() 兩兩垂直.以
兩兩垂直.以![]() 為坐標原點,以
為坐標原點,以![]() 、
、![]() 、
、![]() 為坐標軸建立的空間直角坐標系
為坐標軸建立的空間直角坐標系![]() .
.
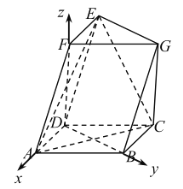
不妨設![]() ,則
,則![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則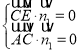 ,則
,則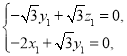 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
∴平面![]() 的一個法向量為
的一個法向量為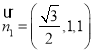 .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則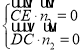 ,則
,則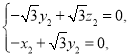 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
∴平面![]() 的一個法向量為
的一個法向量為![]() .
.
∴二面角![]() 的余弦值為
的余弦值為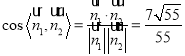 .
.


 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】人們通常以分貝(符號是![]() )為單位來表示聲音強度的等級,30~40分貝是較理想的安靜環境,超過50分貝就會影響睡眠和休息,70分貝以上會干擾談話,長期生活在90分貝以上的嗓聲環境,會嚴重影響聽力和引起神經衰弱、頭疼、血壓升高等疾病,如果突然暴露在高達150分貝的噪聲環境中,聽覺器官會發生急劇外傷,引起鼓膜破裂出血,雙耳完全失去聽力,為了保護聽力,應控制噪聲不超過90分貝,一般地,如果強度為
)為單位來表示聲音強度的等級,30~40分貝是較理想的安靜環境,超過50分貝就會影響睡眠和休息,70分貝以上會干擾談話,長期生活在90分貝以上的嗓聲環境,會嚴重影響聽力和引起神經衰弱、頭疼、血壓升高等疾病,如果突然暴露在高達150分貝的噪聲環境中,聽覺器官會發生急劇外傷,引起鼓膜破裂出血,雙耳完全失去聽力,為了保護聽力,應控制噪聲不超過90分貝,一般地,如果強度為![]() 的聲音對應的等級為
的聲音對應的等級為![]() ,則有
,則有![]() ,則
,則![]() 的聲音與
的聲音與![]() 的聲音強度之比為( )
的聲音強度之比為( )
A.10B.100C.1000D.10000
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]() 相外切,且與直線
相外切,且與直線![]() 相切.
相切.
(1)記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求
,求![]() 的方程;
的方程;
(2)過點![]() 的兩條直線
的兩條直線![]() 與曲線
與曲線![]() 分別相交于點
分別相交于點![]() 和
和![]() ,線段
,線段![]() 和
和![]() 的中點分別為
的中點分別為![]() .如果直線
.如果直線![]() 與
與![]() 的斜率之積等于1,求證:直線
的斜率之積等于1,求證:直線![]() 經過定點.
經過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,若△
,若△![]() 的三個頂點都在拋物線
的三個頂點都在拋物線![]() 上,且
上,且![]() ,則稱該三角形為“核心三角形”.
,則稱該三角形為“核心三角形”.
(1)是否存在“核心三角形”,其中兩個頂點的坐標分別為![]() 和
和![]() ?請說明理由;
?請說明理由;
(2)設“核心三角形”![]() 的一邊
的一邊![]() 所在直線的斜率為4,求直線
所在直線的斜率為4,求直線![]() 的方程;
的方程;
(3)已知△![]() 是“核心三角形”,證明:點
是“核心三角形”,證明:點![]() 的橫坐標小于2.
的橫坐標小于2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(-2,0),B(2,0)為橢圓C的左、右頂點,F為其右焦點,P是橢圓C上異于A,B的動點,且△APB面積的最大值為![]() 。
。
(Ⅰ)求橢圓C的方程;
(Ⅱ)直線AP與橢圓在點B處的切線交于點D,當點P在橢圓上運動時,求證:以BD為直徑的圓與直線PF恒相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司為客戶定制了5個險種:甲,一年期短險;乙,兩全保險;丙,理財類保險;丁,定期壽險:戊,重大疾病保險,各種保險按相關約定進行參保與理賠.該保險公司對5個險種參保客戶進行抽樣調查,得出如下的統計圖例,以下四個選項錯誤的是( )



A.54周歲以上參保人數最少B.18~29周歲人群參保總費用最少
C.丁險種更受參保人青睞D.30周歲以上的人群約占參保人群的80%
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com