
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() 是
是![]() 上的動點,
上的動點,![]() 點滿足
點滿足![]() ,
,![]() 點的軌跡為曲線
點的軌跡為曲線![]() .
.
(Ⅰ)求![]() 的普通方程;
的普通方程;
(Ⅱ)在以![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(I)設出![]() 點的坐標,根據兩個向量相等的坐標表示,求得
點的坐標,根據兩個向量相等的坐標表示,求得![]() 點的坐標,消去參數后得到
點的坐標,消去參數后得到![]() 的普通方程.(II)方法一:先求得直線
的普通方程.(II)方法一:先求得直線![]() 的直角坐標方程,聯立直線的方程和
的直角坐標方程,聯立直線的方程和![]() 的方程,求得交點的坐標,利用兩點間的距離公式求得
的方程,求得交點的坐標,利用兩點間的距離公式求得![]() 的長,進而求得
的長,進而求得![]() 的值.方法二:先求出直線
的值.方法二:先求出直線![]() 的參數方程,將參數方程代入
的參數方程,將參數方程代入![]() 的方程,利用直線參數的幾何意義,求得
的方程,利用直線參數的幾何意義,求得![]() 的值.
的值.
(Ⅰ)設![]() ,
,![]() .
.
∵![]() ∴
∴![]() ,消去
,消去![]() 得
得![]() 的普通方程為
的普通方程為![]() .
.
(Ⅱ)法一:直線的極坐標方程![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,得直線
,得直線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
∴![]() ,由
,由![]() 得
得![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,∴
,∴![]() .
.
法二:直線的極坐標方程![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,得直線
,得直線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
∴![]() .∵直線
.∵直線![]() 的傾斜角為
的傾斜角為![]() ,
,
∴可得直線![]() 的參數方程為
的參數方程為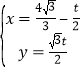 (
(![]() 為參數).
為參數).
代入![]() ,得
,得![]() ,設此方程的兩個根為
,設此方程的兩個根為![]() ,
,![]() ,則
,則![]() .
.
∴![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數![]() ,
,![]() 為常數,且
為常數,且![]() 是函數
是函數![]() 的一個極值點.
的一個極值點.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若函數![]() ,
,![]() ,求
,求![]() 的單調區間;
的單調區間;
(Ⅲ) 過點![]() 可作曲線
可作曲線![]() 的三條切線,求
的三條切線,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天文學中為了衡量星星的明暗程度,古希臘天文學家喜帕恰斯(![]() ,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(
,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(![]() )又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足
)又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足![]() .其中星等為
.其中星等為![]() 的星的亮度為
的星的亮度為![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,則與
倍,則與![]() 最接近的是(當
最接近的是(當![]() 較小時,
較小時, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個圓錐形量杯的高為![]() 厘米,其母線與軸的夾角為
厘米,其母線與軸的夾角為![]() .
.

(1)求該量杯的側面積![]() ;
;
(2)若要在該圓錐形量杯的一條母線![]() 上,刻上刻度,表示液面到達這個刻度時,量杯里的液體的體積是多少.當液體體積是
上,刻上刻度,表示液面到達這個刻度時,量杯里的液體的體積是多少.當液體體積是![]() 立方厘米時,刻度的位置
立方厘米時,刻度的位置![]() 與頂點
與頂點![]() 之間的距離是多少厘米(精確到
之間的距離是多少厘米(精確到![]() 厘米)?
厘米)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在5件產品中,有3件一等品和2件二等品,從中任取2件,以![]() 為概率的事件是( )
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若正四面體PQMN的頂點分別在給定的四面體ABCD的面上,每個面上恰有一個點,那么,( ).
A. 當四面體ABCD是正四面體時,正四面體PQMN有無數個,否則,正四面體PQMN只有一個
B. 當四面體ABCD是正四面體時,正四面體PQMN有無數個,否則,正四面體PQMN不存在
C. 當四面體ABCD的三組對棱分別相等時,正四面體PQMN有無數個,否則,正四面體PQMN只有一個
D. 對任何四面體ABCD,正四面體PQMN都有無數個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3+bx2+cx+d在x=1處取極小值,x=3處取極大值,且函數圖象在(2,f(2))處的切線與直線x-5y=0平行.
(1)求實數abc的值;
(2)設函數f(x)=0有三個不相等的實數根,求d的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如今我們的互聯網生活日益豐富,除了可以很方便地網購,網絡外賣也開始成為不少人日常生活中不可或缺的一部分.某市一調查機構針對該市市場占有率最高的甲、乙兩家網絡外賣企業(以下簡稱外賣甲,外賣乙)的經營情況進行了調查,調查結果如表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外賣甲日接單 | 5 | 2 | 9 | 8 | 11 |
外賣乙日接單 | 2.2 | 2.3 | 10 | 5 | 15 |
(1)據統計表明,![]() 與
與![]() 之間具有線性相關關系.
之間具有線性相關關系.
(ⅰ)請用相關系數![]() 加以說明:(若
加以說明:(若![]() ,則可認為
,則可認為![]() 與
與![]() 有較強的線性相關關系(
有較強的線性相關關系(![]() 值精確到0.001))
值精確到0.001))
(ⅱ)經計算求得![]() 與
與![]() 之間的回歸方程為
之間的回歸方程為![]() .假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于2500單時,外賣甲所獲取的日純利潤的大致范圍:(
.假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于2500單時,外賣甲所獲取的日純利潤的大致范圍:(![]() 值精確到0.01)
值精確到0.01)
(2)試根據表格中這五天的日接單量情況,從平均值和方差角度說明這兩家外賣企業的經營狀況.
相關公式:相關系數 ,
,
參考數據:![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com