
【題目】在平行六面體ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,點M、F分別是線段AA1、BC的中點.
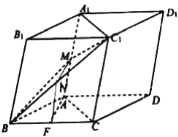
(1)求證:AF⊥DD1;
(2)求證:AF∥平面MBC1.
【答案】(1)見證明(2)見證明
【解析】
(1)由題意可得AF⊥BC.再結合平面![]() 底面
底面![]() ,得到AF⊥平面
,得到AF⊥平面![]() ,
,
可得到AF⊥CC1,根據CC1∥DD1,證得AF⊥DD1.
(2)先根據平行六面體中的線線平行,證出四邊形AFEM是平行四邊形,得到EM // AF,即可證明線面平行.
證明:(1)∵AB![]() AC,點F是線段BC的中點,
AC,點F是線段BC的中點,
∴AF⊥BC.又∵平面![]() 底面
底面![]() ,AF
,AF![]() 平面ABC,
平面ABC,
平面![]() 底面
底面![]() ,
,
∴AF⊥平面![]() .
.
又CC1![]() 平面
平面![]() ,∴AF⊥CC1,
,∴AF⊥CC1,
又CC1∥DD1,∴AF⊥DD1.
(2)連結B1C與BC1交于點E,連結EM,FE.
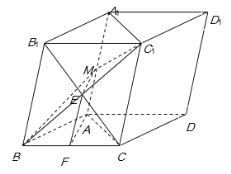
在斜三棱![]() 中,四邊形BCC1B1是平行四邊形,
中,四邊形BCC1B1是平行四邊形,
∴點E為B1C的中點.
∵點F是BC的中點,
∴FE//B1B,FE![]() B1B.
B1B.
又∵點M是平行四邊形BCC1B1邊AA1的中點,
∴AM//B1B,AM![]() B1B.
B1B.
∴AM// FE,AM![]() FE.
FE.
∴四邊形AFEM是平行四邊形.
∴EM // AF.
又EM![]() 平面MBC1,AF
平面MBC1,AF![]() 平面MBC1,
平面MBC1,
∴AF //平面MBC1.


科目:高中數學 來源: 題型:
【題目】人的正常體溫在![]() 至
至![]() 之間,下圖是一位病人在治療期間的體溫變化圖.
之間,下圖是一位病人在治療期間的體溫變化圖.
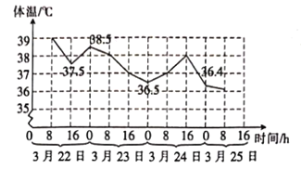
現有下述四個結論:
①此病人已明顯好轉;
②治療期間的體溫極差小于![]() ;
;
③從每8小時的變化來看,25日0時~8時體溫最穩定;
④從3月22日8時開始,每8小時量一次體溫,若體溫不低于![]() 就服用退燒藥,根據圖中信息可知該病人服用了3次退燒藥.
就服用退燒藥,根據圖中信息可知該病人服用了3次退燒藥.
其中所有正確結論的編號是( )
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 過點A
過點A![]() ,兩個焦點為(-1,0),(1,0)。
,兩個焦點為(-1,0),(1,0)。
(Ⅰ)求橢圓C的方程;
(Ⅱ)E,F是橢圓C上的兩個動點,如果直線AE的斜率與AF的斜率互為相反數,證明直線EF的斜率為定值,并求出這個定值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示是一個幾何體的直觀圖、正視圖、俯視圖、側視圖(其中正視圖為直角梯形,俯視圖為正方形,側視圖為直角三角形,尺寸如圖所示).
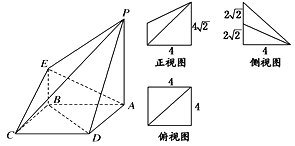
(1)求四棱錐P-ABCD的體積;
(2)證明:BD∥平面PEC;
(3)線段BC上是否存在點M,使得AE⊥PM?若存在,請說明其位置,并加以證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 為函數
為函數![]() 的導函數.
的導函數.
(1)若![]() ,函數
,函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求a、
,求a、![]() 的值;
的值;
(2)若曲線![]() 上存在兩條互相平行的切線,其傾斜角為銳角,求實數
上存在兩條互相平行的切線,其傾斜角為銳角,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知
中,已知![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,且橢圓經過點
的左、右焦點,且橢圓經過點![]() 和點
和點![]() ,其中
,其中![]() 為橢圓的離心率.
為橢圓的離心率.

(1)求橢圓的方程;
(2)過點![]() 的直線
的直線![]() 橢圓于另一點
橢圓于另一點![]() ,點
,點![]() 在直線
在直線![]() 上,且
上,且![]() .若
.若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人的正常體溫在![]() 至
至![]() 之間,下圖是一位病人在治療期間的體溫變化圖.
之間,下圖是一位病人在治療期間的體溫變化圖.

現有下述四個結論:
①此病人已明顯好轉;
②治療期間的體溫極差小于![]() ;
;
③從每8小時的變化來看,25日0時~8時體溫最穩定;
④從3月22日8時開始,每8小時量一次體溫,若體溫不低于![]() 就服用退燒藥,根據圖中信息可知該病人服用了3次退燒藥.
就服用退燒藥,根據圖中信息可知該病人服用了3次退燒藥.
其中所有正確結論的編號是( )
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2alnx.
(1)若函數f(x)的圖象在(2,f(2))處的切線斜率為1,求實數a的值;
(2)若函數![]() 在[1,2]上是減函數,求實數a的取值范圍.
在[1,2]上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了提高職工的健身意識,鼓勵大家加入健步運動,要求200名職工每天晚上9:30上傳手機計步截圖,對于步數超過10000的予以獎勵.圖1為甲乙兩名職工在某一星期內的運動步數統計圖,圖2為根據這星期內某一天全體職工的運動步數做出的頻率分布直方圖.
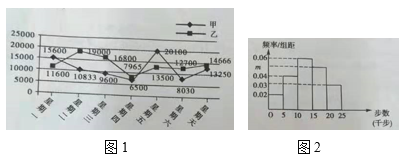
(1)在這一周內任選兩天檢查,求甲乙兩人兩天全部獲獎的概率;
(2)請根據頻率分布直方圖,求出該天運動步數不少于15000的人數,并估計全體職工在該天的平均步數;
(3)如果當天甲的排名為第130名,乙的排名為第40名,試判斷做出的是星期幾的頻率分布直方圖.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com