
已知函數(shù)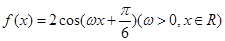 的最小正周期為
的最小正周期為 .
.
⑴求函數(shù) 的對稱軸方程;
的對稱軸方程;
⑵設 ,
, ,求
,求 的值.
的值.
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=4cos ωx· (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(1)求ω的值;
(2)討論f(x)在區(qū)間 上的單調性.
上的單調性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
函數(shù)f(x)=Asin(wx+j)(A>0,w>0,- <j<
<j< ,x∈R)的部分圖象如圖所示:
,x∈R)的部分圖象如圖所示: ,
,
(1)求函數(shù)y=f(x)的解析式;(2)當x∈ 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設向量
 ,定義一種向量積
,定義一種向量積 .
.
已知向量 ,
, ,點
,點 為
為 的圖象上的動點,點
的圖象上的動點,點 為
為 的圖象上的動點,且滿足
的圖象上的動點,且滿足 (其中
(其中 為坐標原點).
為坐標原點).
(1)請用 表示
表示 ;
;
(2)求 的表達式并求它的周期;
的表達式并求它的周期;
(3)把函數(shù) 圖象上各點的橫坐標縮小為原來的
圖象上各點的橫坐標縮小為原來的 倍(縱坐標不變),得到函數(shù)
倍(縱坐標不變),得到函數(shù) 的圖象.設函數(shù)
的圖象.設函數(shù)

 ,試討論函數(shù)
,試討論函數(shù) 在區(qū)間
在區(qū)間 內的零點個數(shù).
內的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
受日月引力影響,海水會發(fā)生漲退潮現(xiàn)象.通常情況下,船在漲潮時駛進港口,退潮時離開港口.某港口在某季節(jié)每天港口水位的深度 (米)是時間
(米)是時間 (
( ,單位:小時,
,單位:小時, 表示0:00—零時)的函數(shù),其函數(shù)關系式為
表示0:00—零時)的函數(shù),其函數(shù)關系式為

 .已知一天中該港口水位的深度變化有如下規(guī)律:出現(xiàn)相鄰兩次最高水位的深度的時間差為12小時,最高水位的深度為12米,最低水位的深度為6米,每天13:00時港口水位的深度恰為10.5米.
.已知一天中該港口水位的深度變化有如下規(guī)律:出現(xiàn)相鄰兩次最高水位的深度的時間差為12小時,最高水位的深度為12米,最低水位的深度為6米,每天13:00時港口水位的深度恰為10.5米.
(1)試求函數(shù) 的表達式;
的表達式;
(2)某貨船的吃水深度(船底與水面的距離)為7米,安全條例規(guī)定船舶航行時船底與海底的距離不小于3.5米是安全的,問該船在當天的什么時間段能夠安全進港?若該船欲于當天安全離港,則它最遲應在當天幾點以前離開港口?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知定義在區(qū)間 上的函數(shù)y=f(x)的圖象關于直線x=-
上的函數(shù)y=f(x)的圖象關于直線x=- 對稱,當x∈
對稱,當x∈ 時,函數(shù)f(x)=Asin(ωx+φ)
時,函數(shù)f(x)=Asin(ωx+φ) 的圖象如圖所示.
的圖象如圖所示.
(1)求函數(shù)y=f(x)在 上的表達式;
上的表達式;
(2)求方程f(x)= 的解.
的解.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設函數(shù)f(x)=sin( -
- )-2cos2
)-2cos2 .
.
(1)求y=f(x)的最小正周期及單調遞增區(qū)間;
(2)若函數(shù)y=g(x)與y=f(x)的圖象關于直線x=2對稱,求當x∈[0,1]時,函數(shù)y=g(x)的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
(2011南京模擬).設 =
=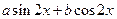 ,其中a,b
,其中a,b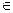 R,ab
R,ab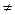 0,若
0,若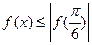 對一切則x
對一切則x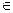 R恒成立,則:①
R恒成立,則:①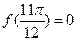 ;②
;②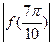 <
<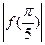 ;③
;③
既不是奇函數(shù)也不是偶函數(shù);④ 的單調遞增區(qū)間是
的單調遞增區(qū)間是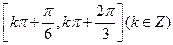 ;⑤存
;⑤存
在經(jīng)過點(a,b)的直線與函數(shù)的圖 像不相交。以上結論正確的是 (寫出所
像不相交。以上結論正確的是 (寫出所
有正確結論的編號)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com