
【題目】新能源汽車已經走進我們的生活,逐漸為大家所青睞.現在有某品牌的新能源汽車在甲市進行預售,預售場面異常火爆,故該經銷商采用競價策略基本規則是:①競價者都是網絡報價,每個人并不知曉其他人的報價,也不知道參與競價的總人數;②競價采用“一月一期制”,當月競價時間截止后,系統根據當期汽車配額,按照競價人的出價從高到低分配名額.某人擬參加2020年6月份的汽車競價,他為了預測最低成交價,根據網站的公告,統計了最近5個月參與競價的人數(如下表)
月份 | 2020.01 | 2020.02 | 2020.03 | 2020.04 | 2020.05 |
月份編號 | 1 | 2 | 3 | 4 | 5 |
競拍人數 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集數據的散點圖發現,可用線性回歸模型擬合競價人數y(萬人)與月份編號t之間的相關關系.請用最小二乘法求y關于t的線性回歸方程:![]() ,并預測2020年6月份(月份編號為6)參與競價的人數;
,并預測2020年6月份(月份編號為6)參與競價的人數;
(2)某市場調研機構對200位擬參加2020年6月份汽車競價人員的報價進行了一個抽樣調查,得到如表所示的頻數表:
報價區間(萬元) |
|
|
|
|
|
|
頻數 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求這200位競價人員報價的平均值![]() 和樣本方差s2(同一區間的報價用該價格區間的中點值代替)
和樣本方差s2(同一區間的報價用該價格區間的中點值代替)
(ii)假設所有參與競價人員的報價X可視為服從正態分布![]() 且μ與σ2可分別由(i)中所示的樣本平均數
且μ與σ2可分別由(i)中所示的樣本平均數![]() 及s2估計.若2020年月6份計劃提供的新能源車輛數為3174,根據市場調研,最低成交價高于樣本平均數
及s2估計.若2020年月6份計劃提供的新能源車輛數為3174,根據市場調研,最低成交價高于樣本平均數![]() ,請你預測(需說明理由)最低成交價.
,請你預測(需說明理由)最低成交價.
參考公式及數據:
①回歸方程![]() ,其中
,其中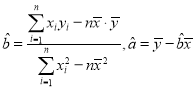
②![]()
③若隨機變量X服從正態分布![]() 則
則![]()
![]() .
.
【答案】(1)![]() ,20000人.(2)(i)11萬元,6.8(ii)13.6萬元
,20000人.(2)(i)11萬元,6.8(ii)13.6萬元
【解析】
(1)利用最小二乘法得出回歸方程,并將![]() 代入回歸方程,即可預測2020年6月份(月份編號為6)參與競價的人數;
代入回歸方程,即可預測2020年6月份(月份編號為6)參與競價的人數;
(2)(i)由頻數表中數據,利用平均數和方差的求解方法求解即可;
(ii)由題意得出競拍成功的概率,根據正態分布的性質,即可確定最低成交價.
解:(1)根據題意,得:![]() ,
,![]()
![]() ,
,![]()
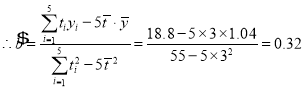
則![]()
從而得到直線的回歸方程為![]()
當![]() 時,
時,![]() .
.
所以預測2020年6月份(月份編號為6)參與競價的人數為20000人.
(2)(i)根據表中給的數據求得平均值和方差為
![]() (萬元).
(萬元).
![]() .
.
(ii)競拍成功的概率為![]()
由題意知![]()
所以![]()
所以![]()
所以2020年6月份的預測的最低成交價![]() 萬元.
萬元.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:
【題目】如圖1,![]() ,點
,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 上靠近
上靠近![]() 的三等分點.現沿
的三等分點.現沿![]() 進行翻折,得到四棱錐
進行翻折,得到四棱錐![]() ,如圖2,且
,如圖2,且![]() .在圖2中:
.在圖2中:
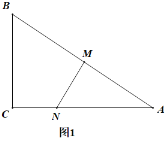

(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】按照水果市場的需要等因素,水果種植戶把某種成熟后的水果按其直徑![]() 的大小分為不同等級.某商家計劃從該種植戶那里購進一批這種水果銷售.為了了解這種水果的質量等級情況,現隨機抽取了100個這種水果,統計得到如下直徑分布表(單位:mm):
的大小分為不同等級.某商家計劃從該種植戶那里購進一批這種水果銷售.為了了解這種水果的質量等級情況,現隨機抽取了100個這種水果,統計得到如下直徑分布表(單位:mm):
d |
|
|
|
|
|
等級 | 三級品 | 二級品 | 一級品 | 特級品 | 特級品 |
頻數 | 1 | m | 29 | n | 7 |
用分層抽樣的方法從其中的一級品和特級品共抽取6個,其中一級品2個.
(1)估計這批水果中特級品的比例;
(2)已知樣本中這批水果不按等級混裝的話20個約1斤,該種植戶有20000斤這種水果待售,商家提出兩種收購方案:
方案A:以6.5元/斤收購;
方案B:以級別分裝收購,每袋20個,特級品8元/袋,一級品5元/袋,二級品4元/袋,三級品3元/袋.
用樣本的頻率分布估計總體分布,問哪個方案種植戶的收益更高?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學共有1000人,其中男生700人,女生300人,為了了解該校學生每周平均體育鍛煉時間的情況以及經常進行體育鍛煉的學生是否與性別有關(經常進行體育鍛煉是指:周平均體育鍛煉時間不少于4小時),現在用分層抽樣的方法從中收集200位學生每周平均體育鍛煉時間的樣本數據(單位:小時),其頻率分布直方圖如圖.已知在樣本數據中,有40位女生的每周平均體育鍛煉時間超過4小時,根據獨立性檢驗原理( )
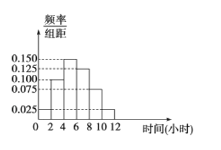
附: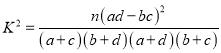 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握認為“該校學生每周平均體育鍛煉時間與性別無關”
B.有90%的把握認為“該校學生每周平均體育鍛煉時間與性別有關”
C.有90%的把握認為“該校學生每周平均體育鍛煉時間與性別無關”
D.有95%的把握認為“該校學生每周平均體育鍛煉時間與性別有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
,![]() 為曲線
為曲線![]() 上一動點,過
上一動點,過![]() 作兩條漸近線的垂線,垂足分別是
作兩條漸近線的垂線,垂足分別是![]() 和
和![]() .
.
(1)當![]() 運動到
運動到![]() 時,求
時,求![]() 的值;
的值;
(2)設直線![]() (不與
(不與![]() 軸垂直)與曲線
軸垂直)與曲線![]() 交于
交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸正半軸交于
軸正半軸交于![]() 點,與
點,與![]() 軸交于
軸交于![]() 點,若
點,若![]() ,
,![]() ,且
,且![]() ,求證
,求證![]() 為定點.
為定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省從2021年開始,高考采用取消文理分科,實行“![]() ”的模式,其中的“1”表示每位學生必須從物理、歷史中選擇一個科目且只能選擇一個科目.某校高一年級有2000名學生(其中女生900人).該校為了解高一年級學生對“1”的選課情況,采用分層抽樣的方法抽取了200名學生進行問卷調查,下表是根據調查結果得到的
”的模式,其中的“1”表示每位學生必須從物理、歷史中選擇一個科目且只能選擇一個科目.某校高一年級有2000名學生(其中女生900人).該校為了解高一年級學生對“1”的選課情況,采用分層抽樣的方法抽取了200名學生進行問卷調查,下表是根據調查結果得到的![]() 列聯表.
列聯表.
性別 | 選擇物理 | 選擇歷史 | 總計 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
總計 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)請你依據該列聯表判斷是否有99.5%的把握認為選擇科目與性別有關?說明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001/span> |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】武漢市掀起了轟轟烈烈的“十日大會戰”,要在10天之內,對武漢市民做一次全員檢測,徹底摸清武漢市的詳細情況.某醫院為篩查冠狀病毒,需要檢驗血液是否為陽性,現有![]() 份血液樣本,有以下兩種檢驗方式:
份血液樣本,有以下兩種檢驗方式:
方案①:將每個人的血分別化驗,這時需要驗1000次.
方案②:按![]() 個人一組進行隨機分組,把從每組
個人一組進行隨機分組,把從每組![]() 個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這
個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這![]() 個人的血就只需檢驗一次(這時認為每個人的血化驗
個人的血就只需檢驗一次(這時認為每個人的血化驗![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進行一次化驗這樣,該組
個人的血樣再分別進行一次化驗這樣,該組![]() 個人的血總共需要化驗
個人的血總共需要化驗![]() 次. 假設此次檢驗中每個人的血樣化驗呈陽性的概率為
次. 假設此次檢驗中每個人的血樣化驗呈陽性的概率為![]() ,且這些人之間的試驗反應相互獨立.
,且這些人之間的試驗反應相互獨立.
(1)設方案②中,某組![]() 個人中每個人的血化驗次數為
個人中每個人的血化驗次數為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設![]() . 試比較方案②中,
. 試比較方案②中,![]() 分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以減少多少次?(最后結果四舍五入保留整數)
分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以減少多少次?(最后結果四舍五入保留整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過點
,過點![]() 作互相垂直的兩條直線分別交橢圓
作互相垂直的兩條直線分別交橢圓![]() 于點
于點![]() (
(![]() 與
與![]() 不重合).
不重合).
(1)證明:直線![]() 過定點
過定點![]() ;
;
(2)若以點![]() 為圓心的圓與直線
為圓心的圓與直線![]() 相切,且切點為線段
相切,且切點為線段![]() 的中點,求四邊形
的中點,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com