Question

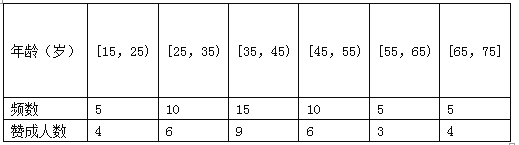
【題目】私家車的尾氣排放是造成霧霾天氣的重要因素之一，因此在生活中我們應該提倡低碳生活，少開私家車，盡量選擇綠色出行方式，為預防霧霾出一份力．為此，很多城市實施了機動車車尾號限行，我市某報社為了解市區(qū)公眾對“車輛限行”的態(tài)度，隨機抽查了50人，將調查情況進行整理后制成下表：

（Ⅰ）完成被調查人員的頻率分布直方圖；

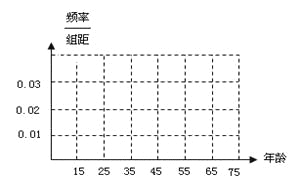
（Ⅱ）若從年齡在[15，25），[25，35）的被調查者中各隨機選取2人進行追蹤調查，求恰有2人不贊成的概率；

（Ⅲ）在（Ⅱ）的條件下，再記選中的4人中不贊成“車輛限行”的人數為，求隨機變量的分布列和數學期望．

Answer 1

【答案】（1）圖見解析

（2）

（3）所以的分布列是：

的數學期望．

【解析】試題分析：（1）由已知求出各組的頻率和縱坐標，由此作出被調查人員的頻率分布直方圖。

（2）由表知年齡在內的有5人，不贊成的有1人，年齡在內的有10人，不贊成的有4人，由此利用互斥事件概率計算公式能求出恰有2人不贊成的概率；

（3）的所有可能取值為，分別求出相應的概率，由此能求出隨機變量的分布列和數學期望。

試題解析：：（Ⅰ）各組的頻率分別為0.1,0.2,0.3，0.2,0.1,0.1，所以圖中各組的縱坐標分別,0.01,0.02,0.03,0.02,0.01,0.01

（Ⅱ）由表知，年齡在內有5人，不贊成的有1人，年齡在內有10人，不贊成的有4人，恰有兩人不贊成的概率為

（Ⅲ）由已知得，的所有取值為0,1,2,3.

所以的分布列是：

所以的數學期望