【題目】已知函數
，曲線在點
處的切線與直線
垂直.
注：
為自然對數的底數.
（1）若函數
在區間
上存在極值，求實數
的取值范圍；
（2）求證：當
時，
.
【答案】（1） 
；（2）見解析.
【解析】
試題分析：（1）求函數
的導數
，由曲線
在點
處的切線與直線
垂直可得
，可求出
的值，這時
，討論導數的符號知函數
僅當
時，取得極值，由
即可求實數
的取值范圍；（2）當
時，
令
，令
，由
證之即可.
試題解析： （1）因為，所以
.………………1分
又據題意，得
，所以
，所以
.………………2分
所以
.
所以.………………3分
當
時，
，為增函數；
當
時，
，
為減函數.
所以函數僅當時，取得極值.………………4分
又函數在區間
上存在極值，所以
，所以
.
故實數
的取值范圍是.………………5分
（2）當時，
，即為.………………6分
令，則
.
再令
，則
.
又因為，所以
.
所以
在
上是增函數.………………7分
又因為
，
所以當時，
.
所以
在區間上是增函數.
所以當時，
，又
，故
.………………9分
令，則
.
因為，所以
.
所以當時，
，故函數
在區間
上是減函數.
又
，………………11分
所以當時，
，
所以
，即
.………………12分
科目：高中數學 來源： 題型：
【題目】一個計算裝置有兩個數據輸入端口I,II與一個運算結果輸出端口III,當I,II分別輸入正整數
時,輸出結果記為
且計算裝置運算原理如下:
①若I,II分別輸入
則
②若I輸入固定的正整數
II輸入的正整數增大
則輸出的結果比原來增大
③若II輸入
I輸入正整數增大
則輸出結果為原來的
倍.則（1）
= 
為正整數)；（2）（1）f（m，1）=__，（2）若由f（m，1）得出f（m，n），則滿足f（m，n）=30的平面上的點（m，n）的個數是__．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從高一年級參加期末考試的學生中抽出50名學生，并統計了他們的數學成績（滿分為100分），將數學成績進行分組，并根據各組人數制成如下頻率分布表：
（1）寫出
的值，并估計本次考試全年級學生的數學平均分（同一組中的數據用該組區間的中點值作代表）；
（2）現從成績在
內的學生中任選出兩名同學，從成績在
內的學生中任選一名同學，共三名同學參加學習習慣問卷調查活動.若
同學的數學成績為43分，
同學的數學成績為
分，求
兩同學恰好都被選出的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高二奧賽班N名學生的物理測評成績（滿分120分）分布直方圖如下，已知分數在100～110的學生數有21人。
（Ⅰ）求總人數N和分數在110～115分的人數n;
（Ⅱ）現準備從分數在110～115分的n名學生（女生占
）中任選2人，求其中恰好含有一名女生的概率；
（Ⅲ）為了分析某個學生的學習狀態，對其下一階段的學習提供指導性建議，對他前7次考試的數學成績x（滿分150分），物理成績y進行分析，下面是該生7次考試的成績。
數學 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知該生的物理成績y與數學成績x是線性相關的，若該生的數學成績達到130分，請你估計他的物理成績大約是多少？
附：對于一組數據
其回歸線
的斜率和截距的最小二乘估計分別為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABCA1B1C1中，AB AC，點E，F分別在棱BB1，CC1上（均異于端點），且∠ABE∠ACF，AE⊥BB1，AF⊥CC1．
求證：（1）平面AEF⊥平面BB1C1C；
（2）BC //平面AEF．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】閱讀如圖所示的程序框圖，解答下列問題：
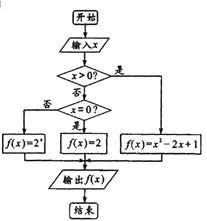
（1）求輸入的
的值分別為
時，輸出的
的值；
（2）根據程序框圖，寫出函數
（
）的解析式；并求當關于
的方程
有三個互不相等的實數解時，實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)與函數g(x)的圖像關于原點對稱，且f(x)=
+2x, 若函數F（x)=g(x)-
f(x)+1在區間
上是增函數，求實數的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
