
【題目】某地一商場記錄了![]() 月份某
月份某![]() 天當中某商品的銷售量
天當中某商品的銷售量![]() (單位:
(單位:![]() )與該地當日最高氣溫
)與該地當日最高氣溫![]() (單位:
(單位:![]() )的相關數據,如下表:
)的相關數據,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)試求![]() 與
與![]() 的回歸方程
的回歸方程![]() ;
;
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;若該地
之間是正相關還是負相關;若該地![]() 月某日的最高氣溫是
月某日的最高氣溫是![]() ,試用所求回歸方程預測這天該商品的銷售量;
,試用所求回歸方程預測這天該商品的銷售量;
(3)假定該地![]() 月份的日最高氣溫
月份的日最高氣溫![]() ,其中
,其中![]() 近似取樣本平均數
近似取樣本平均數![]() ,
,![]() 近似取樣本方差
近似取樣本方差![]() ,試求
,試求![]() .
.
附:參考公式和有關數據 ,
,![]() ,
,![]() ,若
,若![]() ,則
,則![]() ,且
,且![]() .
.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]() .
.
【解析】試題分析:(1)根據表格所給數據及平均數公式可求出![]() 與
與![]() 的值,從而可得樣本中心點的坐標,再求出公式
的值,從而可得樣本中心點的坐標,再求出公式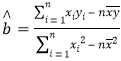 中所需數據,求出
中所需數據,求出![]() ,結合樣本中心點的性質可得
,結合樣本中心點的性質可得![]() ,進而可得
,進而可得![]() 關于
關于![]() 的回歸方程;(2)由
的回歸方程;(2)由![]() 知,
知,![]() 與
與![]() 負相關,將
負相關,將![]() 代入回歸方程即可預測當日銷售量;(3)由(1)知
代入回歸方程即可預測當日銷售量;(3)由(1)知![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() .
.
試題解析:(1)由題意,![]() ,
,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() .
.
所以所求回歸直線方程為![]() .
.
(2)由![]() 知,
知,![]() 與
與![]() 負相關.將
負相關.將![]() 代入回歸方程可得,
代入回歸方程可得,
![]() ,
,
即可預測當日銷售量為![]() .
.
(3)由(1)知![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() .
.
【方法點晴】本題主要考查線性回歸方程及其應用、正態分布的應用,屬于難題.求回歸直線方程的步驟:①依據樣本數據畫出散點圖,確定兩個變量具有線性相關關系;②計算![]() 的值;③計算回歸系數
的值;③計算回歸系數![]() ;④寫出回歸直線方程為
;④寫出回歸直線方程為![]() ; 回歸直線過樣本點中心
; 回歸直線過樣本點中心![]() 是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.
是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
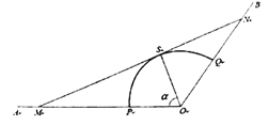
【題目】如圖,射線![]() 和
和![]() 均為筆直的公路,扇形
均為筆直的公路,扇形![]() 區域(含邊界)是一蔬菜種植園,其中
區域(含邊界)是一蔬菜種植園,其中![]() 、
、![]() 分別在射線
分別在射線![]() 和
和![]() 上.經測量得,扇形
上.經測量得,扇形![]() 的圓心角(即
的圓心角(即![]() )為
)為![]() 、半徑為1千米.為了方便菜農經營,打算在扇形
、半徑為1千米.為了方便菜農經營,打算在扇形![]() 區域外修建一條公路
區域外修建一條公路![]() ,分別與射線
,分別與射線![]() 、
、![]() 交于
交于![]() 、
、![]() 兩點,并要求
兩點,并要求![]() 與扇形弧
與扇形弧![]() 相切于點
相切于點![]() .設
.設![]() (單位:弧度),假設所有公路的寬度均忽略不計.
(單位:弧度),假設所有公路的寬度均忽略不計.
(1)試將公路![]() 的長度表示為
的長度表示為![]() 的函數,并寫出
的函數,并寫出![]() 的取值范圍;
的取值范圍;
(2)試確定![]() 的值,使得公路
的值,使得公路![]() 的長度最小,并求出其最小值.
的長度最小,并求出其最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對該校200名高三學生平均每天課外體育鍛煉時間進行調查,如表:(平均每天鍛煉的時間單位:分鐘)

將學生日均課外體育鍛煉時間在![]() 的學生評價為“課外體育達標”.
的學生評價為“課外體育達標”.
(1)請根據上述表格中的統計數據填寫下面的![]() 列聯表;
列聯表;
課外體育不達標 | 課外體育達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
(2)通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關?
參考格式:![]() ,其中
,其中![]()
| 0.025 | 0.15 | 0.10 | 0.005 | 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 2.072 | 6.635 | 7.879 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系中,直線![]() 的參數方程為
的參數方程為![]() ,(
,(![]() 為參數).以原點為極點,
為參數).以原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的極坐標方程與曲線
的極坐標方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知與直線![]() 平行的直線
平行的直線![]() 過點
過點![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點,試求
兩點,試求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】最近,“百萬英雄”,“沖頂大會”等一些闖關答題類游戲風靡全國,既能答題,又能學知識,還能掙獎金。若某闖關答題一輪共有4類題型,選手從前往后逐類回答,若中途回答錯誤,立馬淘汰只能觀戰;若能堅持到4類題型全部回答正確,就能分得現金并獲得一枚復活幣。每一輪闖關答題順序為:1.文史常識類;2.數理常識類;3.生活常識類;4.影視藝術常識類,現從全省高中生中調查了100位同學的答題情況統計如下表:

(Ⅰ)現用樣本的數據特征估算整體的數據特征,從全省高中生挑選4位同學,記![]() 為4位同學獲得獎金的總人數,求
為4位同學獲得獎金的總人數,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若王同學某輪闖關獲得的復活幣,系統會在下一輪游戲中自動使用,即下一輪重新進行闖關答題時,若王同學在某一類題型中回答錯誤,自動復活一次,視為答對該類題型。請問:仍用樣本的數據特征估算王同學的數據特征,那么王同學在獲得復活幣的下一輪答題游戲中能夠最終獲得獎金的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“新零售”模式的背景下,某大型零售公司為推廣線下分店,計劃在![]() 市
市![]() 區開設分店,為了確定在該區設分店的個數,該公司對該市開設分店的其他區的數據做了初步處理后得到下列表格.記
區開設分店,為了確定在該區設分店的個數,該公司對該市開設分店的其他區的數據做了初步處理后得到下列表格.記![]() 表示在各區開設分店的個數,
表示在各區開設分店的個數,![]() 表示這
表示這![]() 個分店的年收入之和.
個分店的年收入之和.

(1)該公司已經過初步判斷,可用線性回歸模型擬合![]() 與
與![]() 的關系,求
的關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)假設該公司在![]() 區獲得的總年利潤
區獲得的總年利潤![]() (單位:百萬元)與
(單位:百萬元)與![]() ,
,![]() 之間的關系為
之間的關系為![]() ,請結合(1)中的線性回歸方程,估算該公司在
,請結合(1)中的線性回歸方程,估算該公司在![]() 區開設多少個分店時,才能使
區開設多少個分店時,才能使![]() 區平均每個分店的年利潤最大?
區平均每個分店的年利潤最大?
參考公式:回歸直線方程為![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com