【題目】對于實數(shù)
符號
表示不超過x的最大整數(shù)，例如
定義函數(shù)
則下列命題正確中的是__________
（1）函數(shù)
的最大值為1；
（2）函數(shù)是增函數(shù)；
（3）方程
有無數(shù)個根；
（4）函數(shù)的最小值為0.
【答案】③④
【解析】
先理解函數(shù)f（x）＝x﹣[x]的含義，再針對選項對該函數(shù)的最值、單調(diào)性以及周期性進(jìn)行分析、判斷正誤即可．
解：對于①，由題意可知f（x）＝x﹣[x]∈[0，1），∴函數(shù)f（x）無最大值，①錯誤；
對于④，由f（x）的值域為[0，1），∴函數(shù)f（x）的最小值為0，④正確；
對于③，函數(shù)f（x）每隔一個單位重復(fù)一次，是以1為周期的函數(shù)，
所以方程f（x）
有無數(shù)個根，③正確；
對于②，函數(shù)f（x）在定義域R上是周期函數(shù)，不是增函數(shù)，②錯誤；
綜上，正確的命題序號是③④．
故答案為：③④．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
是兩條不同的直線，
是兩個不同的平面，有下列正確命題的序號是________．
(1)若m∥
,n∥,則m∥n， (2)若
則
(3)若
，
且
，則
； (4)若
，
，則
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在矩形ABCD中，對角線AC分別與AB，AD所成的角為α，β，則sin2α+sin2β＝1，在長方體ABCD﹣A1B1C1D1中，對角線AC1與棱AB，AD，AA1所成的角分別為α1，α2，α3，與平面AC，平面AB1，平面AD1所成的角分別為β1，β2，β3，則下列說法正確的是（ ）
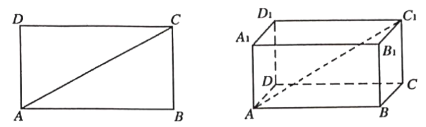
①sin2α1+sin2α2+sin2α3＝1 ②sin2α1+sin2α2+sin2α3＝2
③cos2α1+cos2α2+cos2α3＝1 ④sin2β1+sin2β2+sin2β3＝1
A. ①③B. ②③C. ①③④D. ②③④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，
是圓
內(nèi)一個定點，
是圓上任意一點.線段
的垂直平分線和半徑
相交于點
.
（Ⅰ）當(dāng)點在圓上運動時，點的軌跡
是什么曲線？并求出其軌跡方程；
（Ⅱ）過點
作直線
與曲線交于
、
兩點，點關(guān)于原點
的對稱點為
，求
的面積
的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）若函數(shù)
，試研究函數(shù)
的極值情況；
（2）記函數(shù)
在區(qū)間
內(nèi)的零點為
，記
，若
在區(qū)間
內(nèi)有兩個不等實根
，證明：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某年級組織學(xué)生參加了某項學(xué)術(shù)能力測試,為了解參加測試學(xué)生的成績情況,從中隨機抽取20名學(xué)生的測試成績作為樣本,規(guī)定成績大于或等于80分的為優(yōu)秀,否則為不優(yōu)秀.統(tǒng)計結(jié)果如圖:
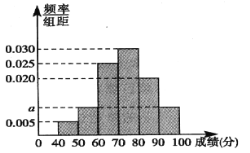
(1)求
的值和樣本的平均數(shù);
(2)從該樣本成績優(yōu)秀的學(xué)生中任選兩名,求這兩名學(xué)生的成績至少有一個落在
內(nèi)的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對于任意
，若數(shù)列
滿足
，則稱這個數(shù)列為“K數(shù)列”.
（1）已知數(shù)列：
，
，
是“K數(shù)列”，求實數(shù)
的取值范圍；
（2）設(shè)等差數(shù)列
的前
項和為
，當(dāng)首項
與公差
滿足什么條件時，數(shù)列
是“K數(shù)列”？
（3）設(shè)數(shù)列的前項和為，
，且
，. 設(shè)
，是否存在實數(shù)
，使得數(shù)列
為“K數(shù)列”. 若存在，求實數(shù)的取值范圍；若不存在，請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
