【題目】天氣預報說，在今后的三天中，每一天下雨的概率均為
，某同學用隨機模擬的方法確定這三天中恰有兩天下雨的概率，該同學利用計算器可以產生0到9之間的取整數值的隨機數，他用1,4,7表示下雨，用0,2,3,5,6,8,9表示不下雨。實驗得出如下20組隨機數：
245,368,590,126,217,895,560,061,378,902
542,751,245,602,156,035,682,148,357,438
請根據該同學實驗的數據確定這三天中恰有兩天下雨的概率為 __________．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓E的長軸的一個端點是拋物線
的焦點，離心率是
．
（1）求橢圓E的方程；
（2）過點
，斜率為k的動直線與橢圓E相交于A、B兩點，請問x軸上是否存在點M，使
為常數？若存在，求出點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
是偶函數.
（1）求證：
是偶函數；
（2）求證：在
上是增函數；
（3）設
（
，且
），若對任意的
，在區間
上總存在兩個不同的數
，
，使得
成立，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】制定投資計劃時，不僅要考慮可能獲得的盈利，而且要考慮可能出現的虧損．某投資人打算投資甲、乙兩個項目．根據預測，甲、乙項目可能的最大盈利率分別為100%和50%，可能的最大虧損分別為30%和10%．投資人計劃投資金額不超過10萬元，要求確保可能的資金虧損不超過1.8萬元．問投資人對甲、乙兩個項目各投資多少萬元，才能使可能的盈利最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為比較甲、乙兩地某月14時的氣溫情況，隨機選取該月中的5天，將這5天中14時的氣溫數據（單位：℃）制成如圖所示的莖葉圖，考慮以下結論：
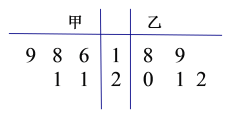
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫；
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫；
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的平均氣溫的標準差；
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的平均氣溫的標準差，
其中根據莖葉圖能得到的統計結論的編號為（ ）
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知各項為正數的數列{an}的前n項和為Sn ， 且滿足 
（Ⅰ）求證：{an}為等差數列，并求數列{an}的通項公式；
（Ⅱ）設 
，求證： 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】微信是現代生活進行信息交流的重要工具，據統計，某公司
名員工中
的人使用微信，其中每天使用微信時間在一小時以內的有
人，其余每天使用微信在一小時以上．若將員工年齡分成青年（年齡小于
歲）和中年（年齡不小于
歲）兩個階段，使用微信的人中
是青年人．若規定：每天使用微信時間在一小時以上為經常使用微信，經常使用微信的員工中
是青年人．
（Ⅰ）若要調查該公司使用微信的員工經常使用微信與年齡的關系，列出
列聯表；
青年人 | 中年人 | 合計 | |
經常使用微信 | |||
不經常使用微信 | |||
合計 |
（Ⅱ）由列聯表中所得數據，是否有
的把握認為“經常使用微信與年齡有關”？
（Ⅲ）采用分層抽樣的方法從“經常使用微信”的人中抽取
人，從這
人中任選
人，求事件
“選出的
人均是青年人”的概率．
附：
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業員工500人參加“學雷鋒”志愿活動，按年齡分組：第1組[25，30)，第2組[30，35)，第3組[35，40)，第4組[40，45)，第5組[45，50]，得到的頻率分布直方圖如圖所示．
(1)上表是年齡的頻數分布表，求正整數
的值；
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人，年齡在第1,2,3組的人數分別是多少？
(3)在(2)的前提下，從這6人中隨機抽取2人參加社區宣傳交流活動，求至少有1人年齡在第3組的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知奇函數f(x)＝
的定義域為R，其中g(x)為指數函數，且過定點(2，9)．
(1)求函數f(x)的解析式；
(2)若對任意的t∈[0，5]，不等式f(t2＋2t＋k)＋f(－2t2＋2t－5)>0恒成立，求實數k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
