
【題目】已知數列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求證:![]() 是等比數列,并求數列
是等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 中是否存在不同的三項按照一定順序重新排列后,構成等差數列?若存在,求滿足條件的項;若不存在,說明理由.
中是否存在不同的三項按照一定順序重新排列后,構成等差數列?若存在,求滿足條件的項;若不存在,說明理由.
【答案】(1)證明見解析,![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)推導出an+1+1=﹣3(an+1),n∈N*.a1+1=2,由此能證明{an+1}是以2為首項,﹣3為公比的等比數列,可求數列{an}通項公式.(2)假設am,an,ap構成等差數列,m≠n≠p,則2an=am+ap,利用(1)的通項公式進行推導不滿足2an=am+ap,從而數列{an}中不存在不同的三項按照一定順序重新排列后,構成等差數列.
(1)因為![]() ,所以
,所以![]() ,因為
,因為![]() ,
,
所以數列![]() 是以2為首項,以-3為公比的等比數列,
是以2為首項,以-3為公比的等比數列,
所以![]() ,即
,即![]() ;
;
(2)假設存在三項![]() 按一定順序重新排列后成等差.
按一定順序重新排列后成等差.
①若![]() ,則
,則![]() ,
,
整理得![]() ,兩邊同除以
,兩邊同除以![]() ,
,
可得![]() ,
,
等式右邊是-3的整數倍,左邊不是-3的整數倍,故等式不成立.
②若![]() ,則
,則![]() ,
,
整理得![]() ,兩邊同除以
,兩邊同除以![]() ,
,
可得![]() ,
,
等式右邊是-3的整數倍,左邊不是-3的整數倍,故等式不成立.
③若![]() ,則
,則![]() ,
,
整理得![]() ,兩邊同除以
,兩邊同除以![]() ,
,
可得![]() ,
,
等式左邊是-3的整數倍,右邊不是-3的整數倍,故等式不成立;
綜上,不存在不同的三項符合題意.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,某公園內有一塊矩形綠地區域ABCD,已知AB=100米,BC=80米,以AD,BC為直徑的兩個半圓內種植花草,其它區域種值苗木. 現決定在綠地區域內修建由直路BN,MN和弧形路MD三部分組成的觀賞道路,其中直路MN與綠地區域邊界AB平行,直路為水泥路面,其工程造價為每米2a元,弧形路為鵝卵石路面,其工程造價為每米3a元,修建的總造價為W元. 設![]() .
.
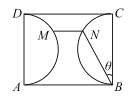
(1)求W關于![]() 的函數關系式;
的函數關系式;
(2)如何修建道路,可使修建的總造價最少?并求最少總造價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次惡劣氣候的飛行航程中調查男女乘客在飛機上暈機的情況,共調查了89位乘客,其中男乘客有24人暈機,31人不暈機;女乘客有8人暈機,26人不暈機
(1)根據此材料數據完成如下的2×2列聯表;
暈機 | 不暈機 | 總計 | |
男人 | |||
女人 | |||
總計 |
(2)根據列聯表,利用下列公式和數據分析,你是否有90%的把握認為在本次飛機飛行中暈機與性別有關?
(3)其中8名暈機的女乘客中有5名是常坐飛機的乘客,另外3名是不常坐飛機的,從這8名乘客中任選3名,這3名乘客不都是常坐飛機的概率是多少?
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式: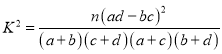 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() ,
,![]() ,…,
,…,![]() 這5個球隊進行單循環比賽(全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場).當比賽進行到一定階段時,統計
這5個球隊進行單循環比賽(全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場).當比賽進行到一定階段時,統計![]() ,
,![]() ,
,![]() ,
,![]() 這4個球隊已經賽過的場數分別為:
這4個球隊已經賽過的場數分別為:![]() 隊4場,
隊4場,![]() 隊3場,
隊3場, ![]() 隊2場,
隊2場,![]() 隊1場,則
隊1場,則![]() 隊比賽過的場數為( )
隊比賽過的場數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,定直線
,定直線![]() :
: ![]() ,動圓
,動圓![]() 過點
過點![]() ,且與直線
,且與直線![]() 相切.
相切.
(Ⅰ)求動圓![]() 的圓心軌跡
的圓心軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線與曲線
的直線與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,分別過點
兩點,分別過點![]() ,
, ![]() 作曲線
作曲線![]() 的切線
的切線![]() ,
, ![]() ,兩條切線相交于點
,兩條切線相交于點![]() ,求
,求![]() 外接圓面積的最小值.
外接圓面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com