
【題目】(導學號:05856307)(12分)
某老師為了分析學生的學習情況,隨機抽取了班上20名學生某次期末考試的成績(滿分為150分)進行分析,統計如下:
男生:133 131 130 126 123 120 116 109 107 105
女生:136 127 125 123 119 118 117 114 113 108
(Ⅰ)計算男、女生成績的平均值并分析比較男、女生成績的分散程度;
(Ⅱ)現從分數在120分以下的女同學中隨機抽取2位,求這兩位同學分數之差的絕對值小于10的概率.
【答案】(1) 男生,女生的平均成績均為120, 男生的成績比較分散,女生的成績比較集中(2) ![]()
【解析】試題分析:(1)計算男女生的平均成績,根據表格數據判斷男女生成績的分散程度;(2)依題意,女生成績在120以下的情況為108,113,114,117,118,119,隨機抽取2人,共15種,其中不滿足條件的為(108,118),(108,119)兩種,從而得到這兩位同學分數之差的絕對值小于10的概率.
試題解析:
(1)男生的平均成績為
![]() =
=![]() (3×130+3×120+110+3×100+1+3+3+6+6+5+7+9)=120,
(3×130+3×120+110+3×100+1+3+3+6+6+5+7+9)=120,
女生的平均成績為
![]() =
=![]() (130+3×120+5×110+100+6+7+5+3+9+8+7+4+3+8)=120,
(130+3×120+5×110+100+6+7+5+3+9+8+7+4+3+8)=120,
所以男、女生的平均成績一樣.由所給數據可以看出,男生的成績比較分散,女生的成績比較集中.
(2) 依題意,女生成績在120以下的情況為108,113,114,117,118,119,
則隨機抽取2人,其成績的情況可能為(108,113),(108,114),(108,117),(108,118),(108,119),(113,114),(113,117),(113,118),(113,119),(114,117),(114,118),(114,119),(117,118),(117,119),(118,119),共15種,其中不滿足條件的為(108,118),(108,119)兩種,故所求概率P=1-![]() =
=![]()


科目:高中數學 來源: 題型:
【題目】(導學號:05856262)
如圖所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中點,AB⊥平面B1C1CB,∠BCC1=60°.
(Ⅰ)求證:AC⊥平面BDC1;
(Ⅱ)E是線段CC1上的動點,判斷點E到平面AA1B1B的距離是否為定值,若是,求出此定值;否則,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
已知曲線C1的參數方程為: ![]() (θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為:
(θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為: ![]() ,直線l的直角坐標方程為
,直線l的直角坐標方程為![]() .
.
(l)求曲線C1和直線l的極坐標方程;
(2)已知直線l分別與曲線C1、曲線C2交異于極點的A,B,若A,B的極徑分別為ρ1,ρ2,求|ρ2﹣ρ1|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像在
的圖像在![]() 上連續不斷,定義:
上連續不斷,定義:
![]() (
(![]() ),
),![]() (
(![]() ),其中
),其中![]() 表示函數
表示函數![]() 在
在![]() 上的最小值,
上的最小值, ![]() 表示函數
表示函數![]() 在
在![]() 上的最大值,若存在最小正整數
上的最大值,若存在最小正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 成立,則稱函數
成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 階收縮函數”.
階收縮函數”.
(1)若![]() ,
, ![]() ,試寫出
,試寫出![]() ,
, ![]() 的表達式;
的表達式;
(2)已知函數![]() ,
, ![]() ,判斷
,判斷![]() 是否為
是否為![]() 上的“
上的“![]() 階收縮函數”,如果是,求出對應的
階收縮函數”,如果是,求出對應的![]() ,如果不是,請說明理由;
,如果不是,請說明理由;
(3)已知![]() ,函數
,函數![]() ,是
,是![]() 上的2階收縮函數,求
上的2階收縮函數,求![]() 的取值范圍.
的取值范圍.
數學附加題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上任意一點到
上任意一點到![]() 的距離比到
的距離比到![]() 軸的距離大1,橢圓
軸的距離大1,橢圓![]() 的中心在原點,一個焦點與
的中心在原點,一個焦點與![]() 的焦點重合,長軸長為4.
的焦點重合,長軸長為4.
(Ⅰ)求曲線![]() 和橢圓
和橢圓![]() 的方程;
的方程;
(Ⅱ)橢圓![]() 上是否存在一點
上是否存在一點![]() ,經過點
,經過點![]() 作曲線
作曲線![]() 的兩條切線
的兩條切線![]() (
(![]() 為切點)使得直線
為切點)使得直線![]() 過橢圓的上頂點,若存在,求出切線
過橢圓的上頂點,若存在,求出切線![]() 的方程,不存在,說明理由.
的方程,不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856312)[選修4-5:不等式選講]
已知函數f(x)=|x-m|-2|x-1|(m∈R).
(Ⅰ)當m=3時,求函數f(x)的最大值;
(Ⅱ)解關于x的不等式f(x)≥0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856330)
已知等比數列{an}的前n項和為Sn,且a3=4,a3,a4+2,a5成等差數列.數列{![]() }的前n項和為Tn.
}的前n項和為Tn.
(Ⅰ)求數列{an}的通項公式以及前n項和Sn的表達式;
(Ⅱ)若Tn<m對任意n∈N*恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
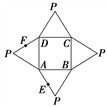
【題目】如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,
在此幾何體中,給出下面四個結論:
①直線BE與直線CF異面; ②直線BE與直線AF異面;
③直線EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 分別為
分別為![]() 的中點,設直線
的中點,設直線![]() 與平面
與平面![]() 交于點
交于點![]() .
.

(1)已知平面![]() 平面
平面![]() ,求證:
,求證: ![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com