
已知 都是正數,
都是正數,
(1)若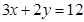 ,求
,求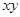 的最大值
的最大值
(2)若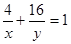 ,求
,求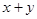 的最小值.
的最小值.
(1)6;(2)36.
解析試題分析:(1)直接利用基本不等式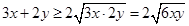 ,
,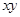 的最大值隨之而定;(2)如果直接利用基本不等式則有
的最大值隨之而定;(2)如果直接利用基本不等式則有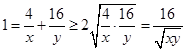 ①,
①,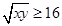 ,因此
,因此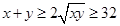 ②,這樣就可能得出
②,這樣就可能得出 的最小值為32,實際上這個最小值是取不到的,因為不等式①取等號的條件是
的最小值為32,實際上這個最小值是取不到的,因為不等式①取等號的條件是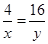 ,
,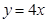 ,不等式②取等號的條件是
,不等式②取等號的條件是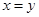 ,即不等式①②不能同時取等號,故
,即不等式①②不能同時取等號,故 的最小值不是32.正確的解法是把
的最小值不是32.正確的解法是把 看作
看作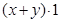 ,把其中的1用已知
,把其中的1用已知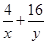 代換,即
代換,即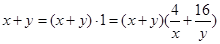 ,展開后就可以直接利用基本不等式求出結果.
,展開后就可以直接利用基本不等式求出結果.
試題解析:(1)xy=·3x·2y≤2=6 4分
當且僅當即時取“=”號.
所以當x=2,y=3時,xy取得最大值6 ..6分
(2)由 且
且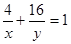 得
得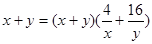

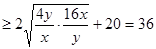 , ..10分
, ..10分
當且僅當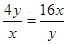 ,即x=12且y=24時,等號成立,
,即x=12且y=24時,等號成立,
所以x+y的最小值是36 12分
考點:基本不等式的應用.


科目:高中數學 來源: 題型:解答題
閱讀:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
當且僅當 ,即
,即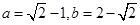 時取到等號,
時取到等號,
則 的最小值為
的最小值為 .
.
應用上述解法,求解下列問題:
(1)已知 ,
, ,求
,求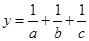 的最小值;
的最小值;
(2)已知 ,求函數
,求函數 的最小值;
的最小值;
(3)已知正數 、
、 、
、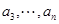 ,
, ,
,
求證: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的定義域為
的定義域為 . 設點P是函數圖象上的任意一點,過點P分別作直線y=x和y軸的垂線,垂足分別為M、N.
. 設點P是函數圖象上的任意一點,過點P分別作直線y=x和y軸的垂線,垂足分別為M、N.
(1)求證: 是定值;
是定值;
(2)判斷并說明 有最大值還是最小值,并求出此最大值或最小值.
有最大值還是最小值,并求出此最大值或最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某化工廠引進一條先進生產線生產某種化工產品,其生產的總成本y(萬元)與年產量x(噸)之間的函數關系式可以近視地表示為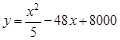 ,已知此生產線的年產量最大為210噸.
,已知此生產線的年產量最大為210噸.
(Ⅰ) 求年產量為多少噸時,生產每噸產品的平均成本最低,并求最低成本;
(Ⅱ)若每噸產品平均出廠價為40萬元,那么當年產量為多少噸時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
若a>0,b>0,a+b=2,則下列不等式對一切滿足條件的a,b恒成立的是 (寫出所有正確命題的編號).
①ab≤1; ② +
+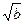 ≤
≤ ; ③a2+b2≥2;
; ③a2+b2≥2;
④a3+b3≥3; 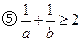 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com