
【題目】已知等差數列{an}的通項公式為an=2n﹣1(n∈N*),且a2 , a5分別是等比數列{bn}的第二項和第三項,設數列{cn}滿足cn= ![]() ,{cn}的前n項和為Sn
,{cn}的前n項和為Sn
(1)求數列{bn}的通項公式;
(2)是否存在m∈N* , 使得Sm=2017,并說明理由
(3)求Sn .
【答案】
(1)解:∵a2=3=b2,a5=9=b3,∴公比q=3
(2)解:不存在m∈N*,使得Sm=2017.∵S7=301<2017,S8=2488>2017,而Sn是單調遞增的,∴不存在m∈N*,使得Sm=2017
(3)解:cn= ![]() ,
,
n為偶數時,Sn= ![]() +
+ ![]() =
= ![]() +
+ ![]() .
.
n為奇數時,Sn= ![]() +
+ ![]() +2n﹣1=
+2n﹣1= ![]() +
+ ![]()
【解析】(1)由a2=3=b2 , a5=9=b3 , 可得公比q.(2).由于S7=301<2017,S8=2488>2017,而Sn是單調遞增的,即可判斷出結論.(3)cn= ![]() ,n為偶數時,Sn=
,n為偶數時,Sn= ![]() +
+ ![]() .n為奇數時,Sn=
.n為奇數時,Sn= ![]() +
+ ![]() +2n﹣1.
+2n﹣1.
【考點精析】本題主要考查了等差數列的前n項和公式的相關知識點,需要掌握前n項和公式:![]() 才能正確解答此題.
才能正確解答此題.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線
軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(2)若曲線![]() 上的所有點都在直線
上的所有點都在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來隨著我國在教育科研上的投入不斷加大,科學技術得到迅猛發展,國內企業的國際競爭力得到大幅提升.伴隨著國內市場增速放緩,國內有實力企業紛紛進行海外布局,第二輪企業出海潮到來.如在智能手機行業,國產品牌已在趕超國外巨頭,某品牌手機公司一直默默拓展海外市場,在海外共設![]() 多個分支機構,需要國內公司外派大量
多個分支機構,需要國內公司外派大量![]() 后、
后、![]() 后中青年員工.該企業為了解這兩個年齡層員工是否愿意被外派工作的態度,按分層抽樣的方式從
后中青年員工.該企業為了解這兩個年齡層員工是否愿意被外派工作的態度,按分層抽樣的方式從![]() 后和
后和![]() 后的員工中隨機調查了
后的員工中隨機調查了![]() 位,得到數據如下表:
位,得到數據如下表:
愿意被外派 | 不愿意被外派 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(Ⅰ)根據調查的數據,是否有![]() 以上的把握認為“是否愿意被外派與年齡有關”,并說明理由;
以上的把握認為“是否愿意被外派與年齡有關”,并說明理由;
(Ⅱ)該公司舉行參觀駐海外分支機構的交流體驗活動,擬安排![]() 名參與調查的
名參與調查的![]() 后、
后、![]() 后員工參加.
后員工參加.![]() 后員工中有愿意被外派的
后員工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人報名參加,從中隨機選出
人報名參加,從中隨機選出![]() 人,記選到愿意被外派的人數為
人,記選到愿意被外派的人數為![]() ;
;![]() 后員工中有愿意被外派的
后員工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人報名參加,從中隨機選出
人報名參加,從中隨機選出![]() 人,記選到愿意被外派的人數為
人,記選到愿意被外派的人數為![]() ,求
,求![]() 的概率.
的概率.
參考數據:
|
|
|
|
|
| |
|
|
|
|
|
|
|
(參考公式:![]() ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期為π.
(1)求f( ![]() )的值;
)的值;
(2)求函數f(x)的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD的底面是矩形,側面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中點,AC與BD的交點為M. 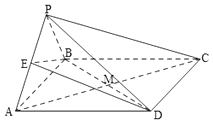
(1)求證:PC∥平面EBD;
(2)求證:BE⊥平面AED.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足Sn=2an+n(n∈N*).
(1)求證數列{an﹣1}是等比數列,并求數列{an}的通項公式;
(2)若bn=log2(﹣an+1),求數列{ ![]() }的前n項和Tn .
}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com