Question

已知單調遞增的等比數列{a_n}滿足：a₂＋a₃＋a₄＝28，且a₃＋2是a₂，a₄的等差中項．
(1)求數列{a_n}的通項公式；
(2)若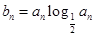，S_n＝b₁＋b₂＋…＋b_n，求使S_n＋n·2^n＋1＞50成立的正整數n的最小值．

Answer 1

（1）a_n＝2ⁿ.  （2）n的最小值為5.　

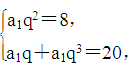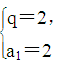解析試題分析：(1)解　設等比數列{a_n}的首項為a₁，公比為q.依題意，有2(a₃＋2)＝a₂＋a₄，代入a₂＋a₃＋a₄＝28，可得a₃＝8，∴a₂＋a₄＝20，所以解之得或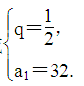又∵數列{a_n}單調遞增，所以q＝2，a₁＝2，∴數列{a_n}的通項公式為a_n＝2ⁿ.(2)因為b_n＝2ⁿlog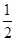2ⁿ＝－n·2ⁿ，所以S_n＝－(1×2＋2×2²＋…＋n·2ⁿ)，2S_n＝－[1×2²＋2×2³＋…＋(n－1)·2ⁿ＋n·2^n＋1]，兩式相減，得
S_n＝2＋2²＋2³＋…＋2ⁿ－n·2^n＋1＝2^n＋1－2－n·2^n＋1.要使S_n＋n·2^n＋1＞50，即2^n＋1－2＞50，即2^n＋1≥52.
易知：當n≤4時，2^n＋1≤2⁵＝32＜52；當n≥5時，2^n＋1≥2⁶＝64＞52.故使S_n＋n·2^n＋1＞50成立的正整數n的最小值為5.　　
考點：等比數列的通項公式
點評：主要是考查了等比數列的通項公式和求和的運用，屬于基礎題。