【題目】
為橢圓
上的點，
是兩焦點，若
，則
的面積是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由題意得，在△F1PF2中，∠F1PF2＝60°，|F1P|+|PF2|＝
＝
，|F1F2|＝4，利用余弦定理可求得|F1P||PF2|的值，從而可求得△PF1F2的面積．
∵橢圓
，∴
＝
，b＝2，c＝2．又∵P為橢圓上一點，∠F1PF2＝60°，
且F1、F2為左右焦點，由橢圓的定義得|F1P|+|PF2|＝＝，|F1F2|＝4，
∴|F1F2|2＝|PF1|
+|PF2|-2|PF1||PF2|cos60°
=（|PF1|+|PF2|）2﹣2|PF1||PF2|﹣2|F1P||PF2|cos60°
＝32﹣3|F1P||PF2|
＝16
∴|F1P||PF2|＝
，∴
＝
|PF1||PF2|sin60°＝××
＝
．
故選：A．
第三學期贏在暑假系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案科目：高中數學 來源： 題型：
【題目】市場份額又稱市場占有率，它在很大程度上反映了企業的競爭地位和盈利能力，是企業非常重視的一個指標.近年來，服務機器人與工業機器人以迅猛的增速占領了中國機器人領域龐大的市場份額，隨著“一帶一路”的積極推動，包括機器人產業在內的眾多行業得到了更廣闊的的發展空間，某市場研究人員為了了解某機器人制造企業的經營狀況，對該機器人制造企業2017年1月至6月的市場份額進行了調查，得到如下資料：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
市場份額 | 11 | 163 | 16 | 15 | 20 | 21 |
請根據上表提供的數據，用最小二乘法求出
關于
的線性回歸方程，并預測該企業2017年7月份的市場份額.
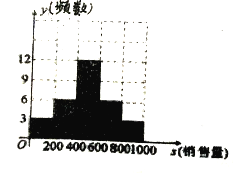
如圖是該機器人制造企業記錄的2017年6月1日至6月30日之間的產品銷售頻數（單位：天）統計圖.設銷售產品數量為
，經統計，當
時，企業每天虧損約為200萬元；
當
時，企業平均每天收入約為400萬元；
當
時，企業平均每天收入約為700萬元.
①設該企業在六月份每天收入為
，求
的數學期望；
②如果將頻率視為概率，求該企業在未來連續三天總收入不低于1200萬元的概率.
附：回歸直線的方程是
，其中
， 
，
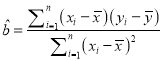查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的導函數為
，且對任意的實數
都有
（
是自然對數的底數），且
，若關于的不等式
的解集中恰有兩個整數，則實數
的取值范圍是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合
為下述條件的函數
的集合：①定義域為
；②對任意實數
，都有
．
（1）判斷函數
是否為中元素，并說明理由；
（2）若函數是奇函數，證明：
；
（3）設和
都是中的元素，求證：
也是中的元素，并舉例說明，
不一定是中的元素．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知圓
過坐標原點
且圓心在曲線
上．
（1）若圓分別與
軸、
軸交于點
（不同于原點），求證：
的面積為定值；
（2）設直線
與圓交于不同的兩點
，且
，求圓的方程；
（3）點
在直線
上，過點引圓（題（2））的兩條切線
，切點為
，求證：直線
恒過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】無窮數列
，若存在正整數
，使得該數列由個互不相同的實數組成，且對于任意的正整數
，
中至少有一個等于
，則稱數列具有性質
.集合
.
（1）若
，
，判斷數列是否具有性質；
（2）數列具有性質，且
，求
的值；
（3）數列具有性質，對于
中的任意元素
，
為第
個滿足
的項，記
，證明：“數列
具有性質”的充要條件為“數列是周期為的周期數列，且每個周期均包含個不同實數”.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數
（
、
為常數且
），滿足條件
，且方程
有等根.
（1）若
，
恒成立，求實數
的取值范圍；
（2）是否存在實數，
，使
當定義域為
時，值域為
？如果存在，求出，
的值；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】由于往屆高三年級數學學科的學習方式大都是“刷題一講題一再刷題”的模式，效果不理想，某市一中的數學課堂教改采用了“記題型一刷題一檢測效果”的模式，并記錄了某學生的記題型時間
（單位：
）與檢測效果
的數據如下表所示.
記題型時間 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
檢測效果 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）據統計表明，與之間具有線性相關關系，請用相關系數
加以說明（若
，則認為與有很強的線性相關關系，否則認為沒有很強的線性相關關系）；
（2）建立關于的回歸方程，并預測該學生記題型的檢測效果；
（3）在該學生檢測效果不低于3.6的數據中任取2個，求檢測效果均高于4.4的概率.
參考公式：回歸直線
中斜率和截距的最小二乘估計分別為
，
，相關系數
參考數據：
，
，
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
