
【題目】已知點(diǎn)A(–1,2),B(2,8)以及![]() ,
,![]() =–13
=–13![]() ,求點(diǎn)C、D的坐標(biāo)和
,求點(diǎn)C、D的坐標(biāo)和![]() 的坐標(biāo).
的坐標(biāo).
【答案】C(38,80),D(–40,–76),![]() =(–78,–156).
=(–78,–156).
【解析】
設(shè)點(diǎn)C、D的坐標(biāo)分別為(x1,y1)、(x2,y2),
由題意得![]() =(x1+1,y1–2),
=(x1+1,y1–2),![]() =(3,6),
=(3,6),![]() =(–1–x2,2–y2),
=(–1–x2,2–y2),![]() =(–3,–6).
=(–3,–6).
因為![]() ,
,![]() ,
,
所以(x1+1,y1–2)=13(3,6),(–1–x2,2–y2)=–13(–3,–6).
所以x1+1=39,y1–2=78,–1–x2=39,2–y2=78,
解得x1=38,y1=80,x2=–40,y2=–76,
所以點(diǎn)C、D的坐標(biāo)分別是(38,80)、(–40,–76),
從而![]() =(–40,–76)–(38,80)=(–78,–156).
=(–40,–76)–(38,80)=(–78,–156).


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩班舉行電腦漢字錄入比賽,參賽學(xué)生每分鐘錄入漢字的個數(shù)經(jīng)統(tǒng)計計算后填入下表,某同學(xué)根據(jù)表中數(shù)據(jù)分析得出的結(jié)論正確的是( )
班級 | 參加人數(shù) | 中位數(shù) | 方差 | 平均數(shù) |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
A.甲、乙兩班學(xué)生成績的平均數(shù)相同
B.甲班的成績波動比乙班的成績波動大
C.乙班優(yōu)秀的人數(shù)多于甲班優(yōu)秀的人數(shù)(每分鐘輸入漢字?jǐn)?shù)≥150個為優(yōu)秀)
D.甲班成績的眾數(shù)小于乙班成績的眾數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4—4:極坐標(biāo)與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,將曲線
中,將曲線![]() (
(![]() 為參數(shù)) 上任意一點(diǎn)
為參數(shù)) 上任意一點(diǎn)![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換 后得到曲線
后得到曲線![]() 的圖形.以坐標(biāo)原點(diǎn)
的圖形.以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線
為極點(diǎn),x軸的非負(fù)半軸為極軸,取相同的單位長度建立極坐標(biāo)系,已知直線![]() .
.
(Ⅰ)求曲線![]() 和直線
和直線![]() 的普通方程;
的普通方程;
(Ⅱ)點(diǎn)P為曲線![]() 上的任意一點(diǎn),求點(diǎn)P到直線
上的任意一點(diǎn),求點(diǎn)P到直線![]() 的距離的最大值及取得最大值時點(diǎn)P的坐標(biāo).
的距離的最大值及取得最大值時點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某投資人欲將5百萬元資金投人甲、乙兩種理財產(chǎn)品,根據(jù)銀行預(yù)測,甲、乙兩種理財產(chǎn)品的收益與投入資金的關(guān)系式分別為![]() ,
,![]() ,其中
,其中![]() 為常數(shù)且
為常數(shù)且![]() .設(shè)對乙種產(chǎn)品投入資金
.設(shè)對乙種產(chǎn)品投入資金![]() 百萬元.
百萬元.
(Ⅰ)當(dāng)![]() 時,如何進(jìn)行投資才能使得總收益
時,如何進(jìn)行投資才能使得總收益![]() 最大;(總收益
最大;(總收益![]() )
)
(Ⅱ)銀行為了吸儲,考慮到投資人的收益,無論投資人資金如何分配,要使得總收益不低于0.45百萬元,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
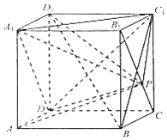
【題目】如圖,點(diǎn)![]() 在正方體
在正方體![]() 的面對角線
的面對角線![]() 上運(yùn)動,則下列四個命題:
上運(yùn)動,則下列四個命題:
①![]() 面
面![]() ;
;
②![]() ;
;
③平面![]() 平面
平面![]() ;
;
④三棱錐![]() 的體積不變.
的體積不變.
其中正確的命題序號是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,求證:函數(shù)
,求證:函數(shù)![]() 只有一個零點(diǎn)
只有一個零點(diǎn)![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下面幾種推理是合情推理的是( )
①由圓的性質(zhì)類比出球的有關(guān)性質(zhì);②由直角三角形、等腰三角形、等邊三角形內(nèi)角和是![]() 歸納出所有三角形的內(nèi)角和都是
歸納出所有三角形的內(nèi)角和都是![]() ;③由
;③由![]() ,滿足
,滿足![]() ,
,![]() ,推出
,推出![]() 是奇函數(shù);④三角形內(nèi)角和是
是奇函數(shù);④三角形內(nèi)角和是![]() ,四邊形內(nèi)角和是
,四邊形內(nèi)角和是![]() ,五邊形內(nèi)角和是
,五邊形內(nèi)角和是![]() ,由此得凸多邊形內(nèi)角和是
,由此得凸多邊形內(nèi)角和是![]() .
.
A. ①②B. ①③④C. ①②④D. ②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]()
![]() (
(![]() )的離心率為
)的離心率為![]() ,且點(diǎn)
,且點(diǎn)![]() 在橢圓
在橢圓![]() 上,設(shè)與
上,設(shè)與![]() 平行的直線
平行的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
, ![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() ,
, ![]() 分別與
分別與![]() 軸正半軸交于
軸正半軸交于![]() ,
, ![]() 兩點(diǎn).
兩點(diǎn).
(I)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)判斷![]() 的值是否為定值,并證明你的結(jié)論.
的值是否為定值,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的一個焦點(diǎn)為
的一個焦點(diǎn)為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程與離心率;
的方程與離心率;
(Ⅱ)設(shè)橢圓![]() 上不與
上不與![]() 點(diǎn)重合的兩點(diǎn)
點(diǎn)重合的兩點(diǎn)![]() ,
, ![]() 關(guān)于原點(diǎn)
關(guān)于原點(diǎn)![]() 對稱,直線
對稱,直線![]() ,
, ![]() 分別交
分別交![]() 軸于
軸于![]() ,
, ![]() 兩點(diǎn).求證:以
兩點(diǎn).求證:以![]() 為直徑的圓被
為直徑的圓被![]() 軸截得的弦長是定值.
軸截得的弦長是定值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com