
���}Ŀ����֪�E�A![]() ���x����
���x����![]() ���E�AC���ϡ�����c(di��n)�քe��A1��A2��������c(di��n)�քe��B1��B2�����ҽ��c(di��n)�քe��F1��F2.ԭ�c(di��n)��ֱ��A2B2�ľ��x��
���E�AC���ϡ�����c(di��n)�քe��A1��A2��������c(di��n)�քe��B1��B2�����ҽ��c(di��n)�քe��F1��F2.ԭ�c(di��n)��ֱ��A2B2�ľ��x��![]() .
.
��1����E�AC�ķ��̣�
��2��P�ǙE�A�Ϯ���A1��A2����һ�c(di��n)��ֱ��PA1��PA2���քe��x�S���c(di��n)N��M����ֱ��OT�c��MN��ֱ���ĈAG���У����c(di��n)��T.�C��������OT���L(zh��ng)�鶨ֵ�������ԓ��ֵ.
���𰸡���1��![]() y2��1��2���C��Ҋ(ji��n)��������ֵ2
y2��1��2���C��Ҋ(ji��n)��������ֵ2
��������
��1���O(sh��)a��2m��c![]() m���tb��m.ֱ��A2B2���̞�mx��2my��2m2��0.���c(di��n)��ֱ�����x��ʽ�����m��1.�ɴ�������E�A����.
m���tb��m.ֱ��A2B2���̞�mx��2my��2m2��0.���c(di��n)��ֱ�����x��ʽ�����m��1.�ɴ�������E�A����.
��2����A1��0��1��A2��0����1�����O(sh��)P��x0��y0�����քe���ֱ��PA1��ֱ��PA2���O(sh��)�AG�ĈA�Ğ�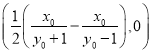 �����ÈA�����|(zh��)���C������OT���L(zh��ng)�Ȟ鶨ֵ2��
�����ÈA�����|(zh��)���C������OT���L(zh��ng)�Ȟ鶨ֵ2��
��1����?y��n)�E�AC���x����e![]() �����O(sh��)a��2m��c
�����O(sh��)a��2m��c![]() m���tb��m.
m���tb��m.
ֱ��A2B2���̞�bx��ay��ab��0����mx��2my��2m2��0.
����![]() �����m��1.
�����m��1.
����a��2��b��1���E�A���̞�![]() y2��1��
y2��1��
��2���ɣ�1����֪A1��0��1��A2��0����1�����O(sh��)P��x0��y0����
ֱ��PA1��y��1![]() x����y��0����xN
x����y��0����xN![]() ��
��
ֱ��PA2��y+1![]() x����y��0����xM
x����y��0����xM![]() ��
��
�O(sh��)�AG�ĈA�Ğ�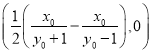 ��
��
�t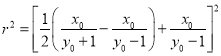
![]()
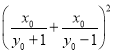 .
.
OG2![]()
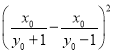 .
.
OT2��OG2��r2![]()
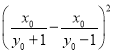
![]()
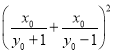
![]() .
.
��![]() y02��1������x02��4��1��y02��������OT2��4��
y02��1������x02��4��1��y02��������OT2��4��
����OT��2��������OT���L(zh��ng)�Ȟ鶨ֵ2.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ИOֵ���Ҍ�(d��o)����(sh��)
�ИOֵ���Ҍ�(d��o)����(sh��)![]() �ĘOֵ�c(di��n)��
�ĘOֵ�c(di��n)��![]() �����c(di��n).
�����c(di��n).
��1����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)�P(gu��n)ϵʽ������(xi��)�����x��
�ĺ���(sh��)�P(gu��n)ϵʽ������(xi��)�����x��
��2���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����������g(sh��)�����������ݷ�����(w��n)�}�������й��岽����ʮ��������(w��n)�����ݷ��Σ���κ�x�r(sh��)�ڔ�(sh��)�W(xu��)�҄������䡶�������g(sh��)ע�������ó������a(b��)ԭ���o�����@��(g��)��(w��n)�}��һ��ⷨ����D1���Ì�(du��)�Ǿ����L(zh��ng)�͌��քe��![]() ��
��![]() �ľ��ηֳɃɂ�(g��)ֱ�������Σ�ÿ��(g��)ֱ���������ٷֳ�һ��(g��)��(n��i)�������Σ��S���̓ɂ�(g��)Сֱ�������Σ��졢�ࣩ�������N�ɫ�ĈD���M(j��n)���ؽM���õ���D2��ʾ�ľ��Σ�ԓ�����L(zh��ng)��
�ľ��ηֳɃɂ�(g��)ֱ�������Σ�ÿ��(g��)ֱ���������ٷֳ�һ��(g��)��(n��i)�������Σ��S���̓ɂ�(g��)Сֱ�������Σ��졢�ࣩ�������N�ɫ�ĈD���M(j��n)���ؽM���õ���D2��ʾ�ľ��Σ�ԓ�����L(zh��ng)��![]() �������(n��i)�������ε�߅�L(zh��ng)
�������(n��i)�������ε�߅�L(zh��ng)![]() ���Ʉ���(g��u)��ĈD��߀���Եõ��S����Ҫ�ĽY(ji��)Փ����D3���O(sh��)
���Ʉ���(g��u)��ĈD��߀���Եõ��S����Ҫ�ĽY(ji��)Փ����D3���O(sh��)![]() ��б߅
��б߅![]() �����c(di��n)����ֱ��������
�����c(di��n)����ֱ��������![]() �ă�(n��i)�������Ό�(du��)�Ǿ�
�ă�(n��i)�������Ό�(du��)�Ǿ�![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���t�����������_���ǣ� ��
���t�����������_���ǣ� ��
���ɈD1�͈D2��e��ȵ�![]() ��
��
����![]() �ɵ�
�ɵ�![]() ��
��
����![]() �ɵ�
�ɵ� ��
��
����![]() �ɵ�
�ɵ�![]() ��
��
A.�٢ڢۢ�B.�٢ڢ�C.�ڢۢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��������ABCD�У�AB��CD��AD��DC��BC��1����ABC��60������߅��ACFE����Σ�ƽ��ACFE��ƽ��ABCD��CF��1��
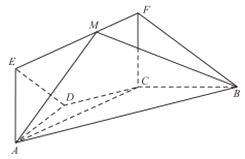
��1���C����BC��ƽ��ACFE��
��2���O(sh��)�c(di��n)M�ھ���EF���\(y��n)��(d��ng)��ƽ��MAB�cƽ��FCB�����J����Ǟ�������cos����ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��![]() ��
��![]() ��(d��o)����(sh��).
��(d��o)����(sh��).
��1����![]() ����
����![]() ��
��![]() ̎���о����̣�
̎���о����̣�
��2����![]() ��
��![]() ���φ��{(di��o)�f������
���φ��{(di��o)�f������![]() ��ȡֵ������
��ȡֵ������
��3�����C����(d��ng)![]() �r(sh��)
�r(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)����Ψһ�O��ֵ�c(di��n).
��(n��i)����Ψһ�O��ֵ�c(di��n).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����(du��)��![]() ��(g��)Ԫ�صĿ��w
��(g��)Ԫ�صĿ��w![]() �M(j��n)�г�ӣ��Ȍ����w�ֳɃɂ�(g��)�ӿ��w
�M(j��n)�г�ӣ��Ȍ����w�ֳɃɂ�(g��)�ӿ��w![]() ��
��![]() ��
��![]() �ǽo����������(sh��)����
�ǽo����������(sh��)����![]() ������?g��u)�ÿ��(g��)�ӿ��w�и��S�C(j��)��ȡ2��(g��)Ԫ�ؽM�ɘӱ�.��
������?g��u)�ÿ��(g��)�ӿ��w�и��S�C(j��)��ȡ2��(g��)Ԫ�ؽM�ɘӱ�.��![]() ��ʾԪ��
��ʾԪ��![]() ��
��![]() ͬ�r(sh��)���F(xi��n)�ژӱ��еĸ���.
ͬ�r(sh��)���F(xi��n)�ژӱ��еĸ���.
��1����![]() �ı��_(d��)ʽ����
�ı��_(d��)ʽ����![]() ��
��![]() ��ʾ����
��ʾ����
��2��������![]() �ĺ�.
�ĺ�.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��
��![]() .
.
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() �D����
�D����![]() ̎���о����̣�
̎���о����̣�
��2����(du��)����![]() ������ʽ
������ʽ![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
��3����![]() ���ژO��ֵ�͘OСֵ���ҘO��ֵС�ژOСֵ����
���ژO��ֵ�͘OСֵ���ҘO��ֵС�ژOСֵ����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����
�酢��(sh��)����![]() ��
��![]() ������
������![]() �ϵ�һ��(d��ng)�c(di��n).
�ϵ�һ��(d��ng)�c(di��n).
��I�����(d��ng)�c(di��n)![]() ��(du��)��(y��ng)�ą���(sh��)��
��(du��)��(y��ng)�ą���(sh��)��![]() ׃��(d��ng)��
׃��(d��ng)��![]() �r(sh��)������
�r(sh��)������![]() �����^(gu��)�ĈD����e��
�����^(gu��)�ĈD����e��
������ֱ��![]() �c����
�c����![]() ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() �龀��
�龀��![]() �����c(di��n)�������ڣ�����c(di��n)
�����c(di��n)�������ڣ�����c(di��n)![]() ����(bi��o)���������ڣ��f(shu��)������.
����(bi��o)���������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() ��
��![]() �ϵ�ż����(sh��)����
�ϵ�ż����(sh��)����![]() ����
����![]() ��
��![]() �φ��{(di��o)�f�p���t����(sh��)
�φ��{(di��o)�f�p���t����(sh��)![]() ��
��![]() ������ ��
������ ��
A. ������(sh��) B. �p����(sh��) C. ������p�ĺ���(sh��) D. �Ȝp�����ĺ���(sh��)
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com