【題目】在直角坐標系xOy中，曲線C的方程為y2=10x，直線l的參數方程為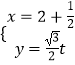 
（t為參數），以坐標原點為極點，以x軸的正半軸為極軸建立極坐標系．
（1）求曲線C的極坐標方程和直線l的普通方程；
（2）設直線l與曲線C交于A、B兩點，求弦長|AB|．
【答案】
（1）解：曲線C的方程為y2=10x，利用互化公式可得：
ρ2sin2θ=10ρcosθ，即ρsin2θ=10cosθ．
直線l的參數方程為 
（t為參數），
消去參數可得： 
x﹣y﹣2 =0．
（2）解：把直線l的參數方程代入曲線C的直角坐標方程可得：3t2﹣20t﹣80=0，
∴t1+t2= 
，t1t2=﹣ 
．
∴|AB|=|t1﹣t2|= 
= 
= 
【解析】（1）曲線C的方程為y2=10x，利用互化公式可得極坐標方程．直線l的參數方程為 （t為參數），消去參數可得普通方程．（2）把直線l的參數方程代入曲線C的直角坐標方程可得：3t2﹣20t﹣80=0，利用|AB|=|t1﹣t2|= 即可得出．
應用題作業本系列答案科目：高中數學 來源： 題型：
【題目】若函數f（x）= 
x3﹣ 
ax2+（a﹣1）x+1在區間（2，3）內為減函數，在區間（5，+∞）為增函數，則實數a的取值范圍是（ ）
A.[3，4]
B.[5，7]
C.[4，6]
D.[7，8]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和Sn=﹣an﹣（ 
）n﹣1+2（n∈N*），數列{bn}滿足bn=2nan ． （Ⅰ）求證數列{bn}是等差數列，并求數列{an}的通項公式；
（Ⅱ）設cn=log2 
，數列{ 
}的前n項和為Tn ， 求滿足Tn 
（n∈N*）的n的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2+（2b﹣1）x+6b﹣a為偶函數，且f（x+1）﹣f（x）=2x+1．
（1）求函數f（x）的解析式；
（2）設g（x）=f（x）+λx，求函數g（x）在[0，1]內的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設α是空間中的一個平面，l，m，n是三條不同的直線，則下列命題中正確的是（ ）
A.若mα，nα，l⊥m，l⊥n，則l⊥α
B.若mα，n⊥α，l⊥n，則l∥m
C.若l∥m，m⊥α，n⊥α，則l∥n
D.若l⊥m，l⊥n，則n∥m
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】二次函數f（x）=ax2+2a是區間[﹣a，a2]上的偶函數，又g（x）=f（x﹣1），則g（0），g（ 
），g（3）的大小關系是（ ）
A.g（ ）＜g（0）＜g（3）
B.g（0）＜g（ ）＜g（3）??
C.g（ ）＜g（3）＜g（0）
D.g（3）＜g（ ）＜g（0）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某中學高三文科班學生共有800人參加了數學與地理的水平測試，學校決定利用隨機數表法從中抽取100人進行成績抽樣調查，先將800人按001，002，…，800進行編號
（1）如果從第8行第7列的數開始向右讀，請你依次寫出最先檢查的3個人的編號；（下面摘取了第7行到第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
（2）抽取的100人的數學與地理的水平測試成績如下表：
成績分為優秀、良好、及格三個等級；橫向，縱向分別表示地理成績與數學成績，例如：表中數學成績為良好的共有
.
①若在該樣本中，數學成績優秀率是30%，求
的值：
人數 | 數學 | |||
優秀 | 良好 | 及格 | ||
地理 | 優秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 |
| 4 |
| |
②在地理成績及格的學生中，已知
， 
，求數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
已知函數
，
．
（1）若曲線
在點
處的切線與直線
垂直，求
的值；
（2）若
存在極小值
時，不等式
恒成立，求實數
的取值范圍；
（3）當
時，如果存在兩個不相等的正數
，使得
，求證：
．
請考生在第22、23兩題中任選一題作答．注意：只能做所選定的題目.如果多做，則按所做的第一個題目計分．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
