【題目】已知公差不為零的等差數列{an}中， S2＝16，且
成等比數列.
（1）求數列{an}的通項公式；
（2）求數列{|an|}的前n項和Tn.
【答案】（1）an＝11－2n(n∈N*)．（2）見解析．
【解析】
(1)S2＝16，
成等比數列，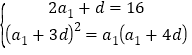
解得首項和公差進而得到通項；（2）當n≤5時，Tn＝a1＋a2＋…＋an, 直接按照等差數列求和公式求和即可, n≥6,Tn＝a1＋a2＋…＋a5－a6－a7－ …－an =n2－10n＋50,寫成分段即可.
（1）由S2＝16，成等比數列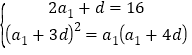，得解得
所以等差數列{an}的通項公式為an＝11－2n(n∈N*)．
（2）當n≤5時，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋an＝Sn＝－n2＋10n.
當n≥6時，Tn＝|a1|＋|a2|＋…＋|an|＝a1＋a2＋…＋a5－a6－a7－ …－an＝2S5－Sn＝2×(－52＋10×5)－(－n2＋10n)＝n2－10n＋50，
故Tn＝
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
（a＞0，且a≠1）在R上單調遞減，且關于x的方程|f（x）|=2﹣x恰好有兩個不相等的實數解，則a的取值范圍是（ ）
A.（0， 
]
B.[ ， 
]
C.[ 
， ]∪{ }
D.[ ， ）∪{ }
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=sin（2x+φ）（|φ|＜π）的圖象向左平移 
個單位后關于原點對稱，則函數f（x）在[0， 
]上的最小值為（ ）
A.﹣ 
B.﹣ 
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在外接圓直徑為1的△ABC中，角A，B，C的對邊分別為a，b，c，設向量 
=（a，cosB）， 
=（b，cosA），且 ∥ ， ≠ ．
（1）求sinA+sinB的取值范圍；
（2）若abx=a+b，試確定實數x的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分） 某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如下表（假設該區域空氣質量指數不會超過
）：
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 |
|
|
|
|
|
|
該社團將該校區在
年
天的空氣質量指數監測數據作為樣本，繪制的頻率分布直方圖如下圖，把該直方圖所得頻率估計為概率．
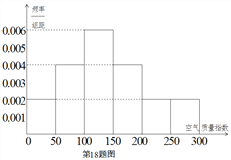
（Ⅰ）請估算
年（以
天計算）全年空氣質量優良的天數(未滿一天按一天計算)；
（Ⅱ）該校
年
月
、
日將作為高考考場，若這兩天中某天出現
級重度污染，需要凈化空氣費用
元，出現
級嚴重污染，需要凈化空氣費用
元，記這兩天凈化空氣總費用為
元，求
的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
，在
處的切線方程為
.
（1）求
， 
；
（2）若
，證明： 
.
【答案】（1）
， 
；（2）見解析
【解析】試題分析：（1）求出函數的導數，得到關于
的方程組，解出即可；
（2）由（1）可知
， 
，
由
，可得
，令
， 利用導數研究其單調性可得
，
從而證明
.
試題解析：（（1）由題意
，所以
，
又
，所以
，
若
，則
，與
矛盾，故
， 
.
（2）由（1）可知
， 
，
由
，可得
，
令
，
，
令
當
時， 
， 
單調遞減，且
；
當
時， 
， 
單調遞增；且
，
所以
在
上當單調遞減，在
上單調遞增，且
，
故
，
故
.
【點睛】本題考查利用函數的切線求參數的方法，以及利用導數證明不等式的方法，解題時要認真審題，注意導數性質的合理運用.
【題型】解答題
【結束】
22
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
， 
為參數），以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
，若直線
與曲線
相切；
（1）求曲線
的極坐標方程；
（2）在曲線
上取兩點
， 
與原點
構成
，且滿足
，求面積
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列
中，
在直線
．
（1）求數列{an}的通項公式；
（2）令
，數列
的前n項和為
．
（ⅰ）求；
（ⅱ）是否存在整數λ
，使得不等式(－1)nλ＜
(n∈N
)恒成立？若存在，求出λ的取值的集合；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
